(本小题满分15分)已知函数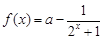 ,
,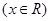 .
.
(1)用定义证明:不论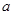 为何实数
为何实数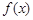 在
在 上为增函数;
上为增函数;
(2)若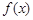 为奇函数,求
为奇函数,求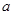 的值;
的值;
(3)在(2)的条件下,求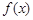 在区间[1,5]上的最小值.
在区间[1,5]上的最小值.
(本小题满分12分)如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20 m,求山高CD.
已知函数 的值满足
的值满足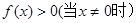 ,对任意实数x、y都有
,对任意实数x、y都有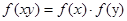 ,且f(-1)=1,f(27)=9,当0<x<1时,
,且f(-1)=1,f(27)=9,当0<x<1时,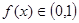 .
.
(1)求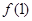 的值,判断
的值,判断 的奇偶性并证明;
的奇偶性并证明;
(2)判断 在(0,+∞)上的单调性,并给出证明;
在(0,+∞)上的单调性,并给出证明;
(3)若 且
且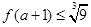 ,求a的取值范围。
,求a的取值范围。
(满分13分)已知奇函数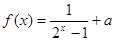 。
。
(1)求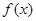 的定义域;(2)求a的值;(3)证明
的定义域;(2)求a的值;(3)证明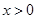 时,
时,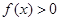
(满分12分)有一个自来水厂,蓄水池有水450吨. 水厂每小时可向蓄水池注水80吨,同时蓄水池又向居民小区供水,t小时内供水量为160 吨. 现在开始向池中注水并同时向居民供水. 问多少小时后蓄水池中水量最少?并求出最少水量.
吨. 现在开始向池中注水并同时向居民供水. 问多少小时后蓄水池中水量最少?并求出最少水量.
已知二次函数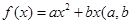 为常数,且
为常数,且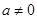 )满足条件:
)满足条件: ,且方程
,且方程 有两等根.
有两等根.
(1)求 的解析式;
的解析式;
(2)求 在
在 上的最大值.
上的最大值.