(本小题满分12分)
已知等差数列{ }的前项和为
}的前项和为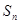 ,且
,且 。数列
。数列 为等比数列,且首项
为等比数列,且首项 ,
, .
.
(1)求数列 ,
, 的通项公式;
的通项公式;
(2)若数列 满足
满足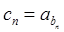 ,求数列
,求数列 的前
的前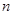 项和为
项和为 ;
;
设计一幅宣传画,要求画面面积为4840 cm2,画面的宽与高的比为λ(λ<1),画面的上、下各留8 cm的空白,左右各留5 cm空白,怎样确定画面的高与宽尺寸,才能使宣传画所用纸张面积最小?如果λ∈[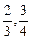 ],怎样确定画面的高与宽尺寸,才能使宣传画所用纸张面积最小?
],怎样确定画面的高与宽尺寸,才能使宣传画所用纸张面积最小?
在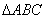 中,角
中,角 所列边分别为
所列边分别为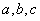 ,且
,且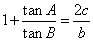
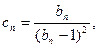
(Ⅰ)求角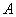 ;
;
(Ⅱ)若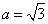 ,试判断
,试判断 取得最大值时
取得最大值时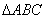 形状
形状
已知
(1)解关于 的不等式
的不等式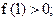

(2)若不等式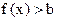 的解集为
的解集为 求实数
求实数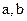 的值 .
的值 .
已知等差数列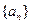 的前
的前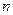 项和为
项和为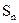 ,且
,且 .
.
(Ⅰ)求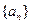 的通项公式;
的通项公式;
(Ⅱ)设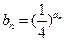 ,求证:
,求证: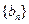 是等比数列,并求其前
是等比数列,并求其前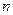 项和
项和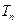 .
.
已知定义在实数集上的函数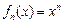 ,
,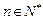 ,其导函数记为
,其导函数记为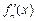 ,且满足:
,且满足: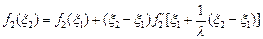
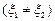 ,
,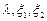 为常数.
为常数.
(Ⅰ)试求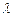 的值;
的值;
(Ⅱ)设函数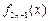 与
与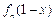 的乘积为函数
的乘积为函数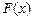 ,求
,求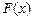 的极大值与极小值;
的极大值与极小值;
(Ⅲ)试讨论关于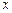 的方程
的方程 在区间
在区间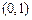 上的实数根的个数.
上的实数根的个数.