一个质量为m,电荷量为-q,不计重力的带电粒子从x轴上的P(a,0)点以速度v,沿与x正方向成60°的方向射入第一象限内的匀强磁场中,并恰好垂直于y轴射出第一象限。求匀强磁场的磁感应强度B和穿过第一象限的时间。
有一平板车,车厢底板光滑,车厢的前后端均有挡板,前后挡板间的距离L=10m。将一个小物体放在底板上并靠着后挡板,让平板车在平直轨道上由静止开始做匀加速直线运动,加速度a1=2m/s2。经时间t1= 4s,平板车开始刹车,平板车立即开始做匀减速直线运动,加速度大小a2=4m/s2,求:
(1)平板车刚开始刹车时的速度v
(2)平板车从开始运动到停止运动通过的位移x
(3)从平板车开始刹车至小物体撞到平板车的前挡板经历的时间t
一辆汽车从静止开始沿直线匀加速开出,然后保持做匀速直线运动,最后做匀减速直线运动直到停止。从汽车开始运动起开始计时,下表给出了某些时刻汽车的瞬时速度,根据表中的数据求:
| 时刻(s) |
1.0 |
2.0 |
3.0 |
5.0 |
7.0 |
9.5 |
10.5 |
| 速度(m/s) |
3.0 |
6.0 |
9.0 |
12 |
12 |
9. 0 |
3.0 |
(1)汽车做匀加速直线运动的加速度和时间
(2)汽车做匀速直线运动经历的时间
如图所示,轻绳悬挂质量为m的小球,用水平力F拉小球使绳与竖直方向成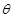 角,小球处于平衡状态。
角,小球处于平衡状态。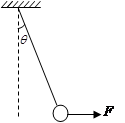
(1)在答题卡相应位置画出小球的受力分析图;
(2)求力F和绳对小球的拉力FT的大小。
如图所示,两块水平放置、相距为d的长金属板接在电压可调的电源上。两板之间的右侧区域存在方向垂直纸面向里的匀强磁场。将喷墨打印机的喷口放置在两极板的正中央处,从喷口连续不断喷出质量均为m、水平速度大小均为v0、带电荷量为q的墨滴,调节电源电压,使墨滴在电场区域恰能沿中心线水平向右做匀速直线运动;进入电场和磁场共存区域后,最终打在上极板的P点,且速度方向与上极板成53°角。(sin53°=0.8,cos53°=0.6)。
(1)判断墨滴所带电荷的种类,并求出两板间的电压;
(2)求磁感应强度B的值。
如图所示,在匀强磁场中有一倾斜的光滑平行金属导轨,导轨间距为L=1m,导轨长为d=3m,导轨平面与水平面的夹角为θ=300,匀强磁场的磁感应强度大小为B=1T,方向与导轨平面垂直向上,质量为m=0.1Kg的导体棒从导轨的顶端由静止开始释放,导棒在滑至底端之前已经做匀速运动,设导体棒始终与导轨垂直,并与导轨接触良好,接在两导轨间的电阻为R=2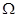 ,其他部分的电阻均不计,重力加速度g=10m/s2。求:
,其他部分的电阻均不计,重力加速度g=10m/s2。求: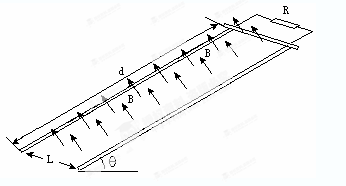
(1)导体棒匀速运动时的速度v大小;
(2)导体棒从导轨的顶端运动到底端的整个过程中,电阻R产生的焦耳热Q。