(本小题满分16分)
已知圆C过点P(1,1),且与圆M: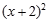 +
+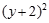 =
=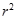 (r>0)关于直线x+y+2=0对称.
(r>0)关于直线x+y+2=0对称.
(1)求圆C的方程;
(2)直线l过点Q(1,0.5),截圆C所得的弦长为2,求直线l的方程;
(3)过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
(本题12分)
在 中,角
中,角 所对的边为
所对的边为 已知
已知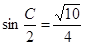 .
.
(1)求 的值;
的值;
(2)若 的面积为
的面积为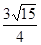 ,且
,且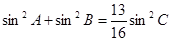 ,求
,求 的值.
的值.
(本题12分)某公司是专门生产健身产品的企业,第一批产品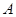 上市销售40天内全部售完,该公司对第一批产品
上市销售40天内全部售完,该公司对第一批产品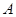 上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品
上市后的市场销售进行调研,结果如图(1)、(2)所示.其中(1)的抛物线表示的是市场的日销售量与上市时间的关系;(2)的折线表示的是每件产品 的销售利润与上市时间的关系.
的销售利润与上市时间的关系.
(1)写出市场的日销售量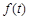 与第一批产品A上市时间t的关系式;
与第一批产品A上市时间t的关系式;
(2)第一批产品A上市后的第几天,这家公司日销售利润最大,最大利润是多少?
(本题12分)
设命题P:函数 在区间[-1,1]上单调递减;命题q:函数
在区间[-1,1]上单调递减;命题q:函数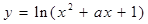 的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
的值域是R.如果命题p或q为真命题,p且q为假命题,求a的取值范围.
(本题12分)
已知函数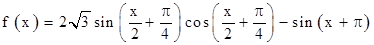 。
。
(1)求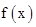 的最小正周期;
的最小正周期;
(2)若将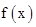 的图象按向量
的图象按向量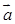 =(
=(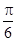 ,0)平移得到函数g(x)的图象,求函数g(x)在区间
,0)平移得到函数g(x)的图象,求函数g(x)在区间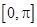 上的最大值和最小值。
上的最大值和最小值。
(本小题14分)设函数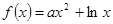 .
.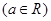
(Ⅰ)讨论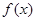 的单调性;
的单调性;
(Ⅱ)已知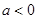 ,若函数
,若函数 的图象总在直线
的图象总在直线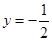 的下方,求
的下方,求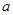 的取值范围;
的取值范围;
(Ⅲ)记 为函数
为函数 的导函数.若
的导函数.若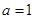 ,试问:在区间
,试问:在区间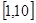 上是否存在
上是否存在 (
(
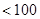 )个正数
)个正数 …
… ,使得
,使得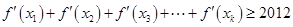 成立?请证明你的结论.
成立?请证明你的结论.