统计表明，某种型号的汽车在匀速行驶中每小时的耗油量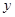
（升）关于行驶速度
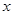（千米/小时）的函数解析式可以表示为：
已知甲、乙两地相距100千米。
（I）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（II）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
设数列{an}是公比为正数的等比数列，a1=2，a3﹣a2=12．
（1）求数列{an}的通项公式；
（2）设数列{bn}是首项为1，公差为2的等差数列，求数列{an+bn}的前n项和Sn．
已知函数f（x）=|x﹣4|﹣t，t∈R，且关于x的不等式f（x+2）≤2的解集为[﹣1，5]．
（1）求t值；
（2）a，b，c均为正实数，且a+b+c=t，求证：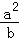
+
+
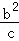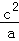≥1．
在直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴建立极坐标系，已知圆C的圆心的极坐标为（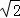
，
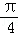），半径r=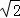，点P的极坐标为（2，π），过P作直线l交圆C于A，B两点．
（1）求圆C的直角坐标方程；（2）求|PA|•|PB|的值．
如图，已知AB是⊙O的直径，CD是⊙O的切线，C为切点，连接AC，过点A作AD⊥CD于点D，交⊙O于点E．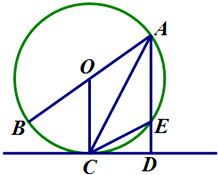
（Ⅰ）证明：∠AOC=2∠ACD；（Ⅱ）证明：AB•CD=AC•CE．
已知函数f（x）=ex﹣m﹣ln（2x）．
（Ⅰ）设x=1是函数f（x）的极值点，求m的值并讨论f（x）的单调性；
（Ⅱ）当m≤2时，证明：f（x）＞﹣ln2．