已知关于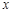
的方程
有实数根
．
（1）求实数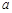
，的值；
（2）若复数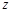
满足
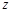，求为何值时，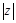
有最小值并求出最小值．
已知函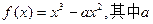数
为正常数。
（1）设当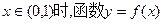
图象上任一点P处的切线的斜率为k，若
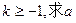的取值范围；
（2）当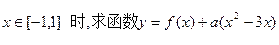
的最大值。
（（本小题满分14分）已知圆O：
直线
。
（I）求圆O上的点到直线
的最小距离。
|
（II）设圆O与
轴的两交点是F1、F2，若从F1发出的光线经上的点M反射后过点F2，求以F1、F2为焦点且经过点M的椭圆方程。
已知圆C经过P（4，– 2），Q（– 1，3）两点，且在y轴上截得的线段长为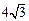
，半径小于5．
（1）求直线PQ与圆C的方程．
（2）若直线l∥PQ，且l与圆C交于点A、B，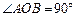
，求直线l的方程．
（
已知过点A（0，2），且方向向量为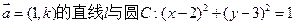
，相交于M、N两点.
（1）求实数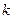
的取值范围:
（2）若O为坐标原点，且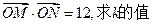
.
数列{an}的前n项和记为Sn，已知a1=1,an+1=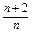
Sn(n=1,2,3，…)．
证明：(1)．数列{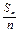
}是等比数列；(2)．Sn+1=4an.