某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。 请回答:
(1)设每件衬衫降价x元,则商场平均每天可多售出 件,每件赢利 元(用含x的代数式表示);
(2)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
某市政部门为了保护生态环境,计划购买 , 两种型号的环保设备.已知购买一套 型设备和三套 型设备共需230万元,购买三套 型设备和两套 型设备共需340万元.
(1)求 型设备和 型设备的单价各是多少万元;
(2)根据需要市政部门采购 型和 型设备共50套,预算资金不超过3000万元,问最多可购买 型设备多少套?
对垃圾进行分类投放,能提高垃圾处理和再利用的效率,减少污染,保护环境.为了检查垃圾分类的落实情况,某居委会成立了甲、乙两个检查组,采取随机抽查的方式分别对辖区内的 , , , 四个小区进行检查,每个检查组随机抽查两个小区,并且每个小区不重复检查.
(1)甲组抽到 小区的概率是 ;
(2)请用列表或画树状图的方法求甲组抽到 小区,同时乙组抽到 小区的概率.
为了响应“学习强国,阅读兴辽”的号召,某校鼓励学生利用课余时间广泛阅读,学校打算购进一批图书.为了解学生对图书类别的喜欢情况,校学生会随机抽取部分学生进行问卷调查,规定被调查学生从“文学、历史、科学、生活”中只选择自己最喜欢的一类,根据调查结果绘制了下面不完整的统计图.
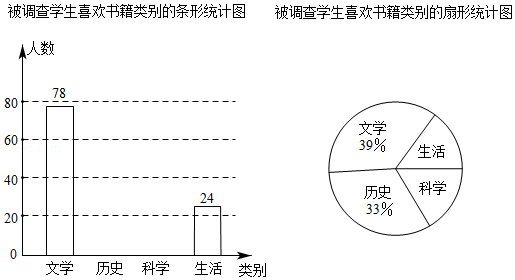
请根据图表信息,解答下列问题.
(1)此次共调查了学生 人;
(2)请通过计算补全条形统计图;
(3)若该校共有学生2200人,请估计这所学校喜欢“科学”类书的学生人数.
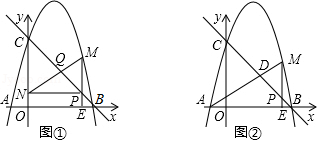
如图,直线 与 轴交于点 ,与 轴交于点 ,抛物线 经过 , 两点,与 轴另一交点为 .点 以每秒 个单位长度的速度在线段 上由点 向点 运动(点 不与点 和点 重合),设运动时间为 秒,过点 作 轴垂线交 轴于点 ,交抛物线于点 .
(1)求抛物线的解析式;
(2)如图①,过点 作 轴垂线交 轴于点 ,连接 交 于点 ,当 时,求 的值;
(3)如图②,连接 交 于点 ,当 是等腰三角形时,直接写出 的值.
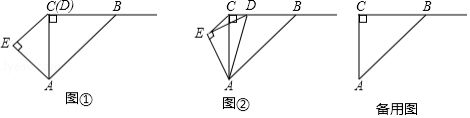
如图, 是等腰直角三角形, , 是射线 上一点(点 不与点 重合),以 为斜边作等腰直角三角形 (点 和点 在 的同侧),连接 .
(1)如图①,当点 与点 重合时,直接写出 与 的位置关系;
(2)如图②,当点 与点 不重合时,(1)的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;
(3)当 时,请直接写出 的值.