已知
是函数
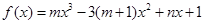的一个极值点，其中
，
（I）求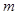
与
的关系式；
（II）求
的单调区间；
（III）当
时，函数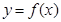
的图象上任意一点的切线斜率恒大于3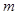，求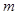的取值范围.
如图，已知椭圆
的离心率为
，且经过点
平行于
的直线
在
轴上的截距为
，与椭圆有A、B两个
不同的交点
（Ⅰ） 求椭圆的方程；
(Ⅱ)求
的取值范围；
（III）求证:直线
、
与
轴始终围成一个等腰三角形．
若数列
的前
项和为
：；
（Ⅰ） 求数列的通项公式
；
(Ⅱ) 设数列
的前项和为
，是否存在实数
，使得
对一切正整数都成立?若存在,求出的最小值,若不存在,请说明理由．
如图（1），
是等腰直角三角形，
，
、
分别为
、
的中点，将
沿
折起，使
在平面
上的射影
恰为
的中点，得到图（2）．
（Ⅰ）求证：
；(Ⅱ)求三棱锥
的体积．
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表：
性别与看营养说明列联表单位: 名
| 男 |
女 |
总计 |
|
| 看营养说明 |
50 |
30 |
80 |
| 不看营养说明 |
10 |
20 |
30 |
| 总计 |
60 |
50 |
110 |
（I）从这50名女生中按是否看营养说明采取分层抽样，抽取一个容量为
的样本，问样本中看与不看营养说明的女生各有多少名?
(Ⅱ)从（I）中的5名女生样本中随机选取两名作深度访谈, 求选到看与不看营养说明的女生各一名的概率；
（III）根据以上列联表，问有多大把握认为“性别与在购买食物时看营养说明”有关？