某班有50名学生,在学校组织的一次数学质量抽测中,如果按照抽测成绩的分数段[60,65),[65,70),…,[95,100)进行分组,得到的分布情况如图3所示.求: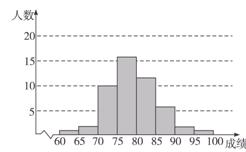
图3
(1)该班抽测成绩在[70,85)之间的人数;
(2)该班抽测成绩不低于85分的人数占全班总人数的百分比.
从个体数为103的总体中采用系统抽样,抽取一个容量为10的样本.写出具体的操作方法.
甲、乙两人进行射击比赛,在一轮比赛中,甲、乙各射击一发子弹。根据以往资料知,甲击中8环,9环,10环的概率分别为0.6,0.3,0.1,乙击中8环,9环,10环的概率分别为0.4,0.4,0.2。
设甲、乙的射击相互独立。
(Ⅰ)求在一轮比赛中甲击中的环数多于乙击中环数的概率;
(Ⅱ)求在独立的三轮比赛中,至少有两轮甲击中的环数多于乙击中环数的概率。
已知双曲线方程为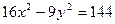 ,
,
①求该双曲线的实轴长、虚轴长、离心率、准线方程;
②若抛物线 的顶点是该双曲线的中心,而焦点是其左顶点,求抛物线
的顶点是该双曲线的中心,而焦点是其左顶点,求抛物线 的方程。
的方程。
已知 ,函数
,函数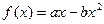 。
。
(1)求证: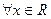 均有
均有 是
是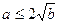 的充分条件;
的充分条件;
(2)当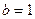 时,求
时,求 恒成立的充要条件。
恒成立的充要条件。