工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只派一次,工作时间不超过10分钟,如果前一个人10分钟内不能完成任务则撤出,再派下一个人,现在一共只有甲、乙、丙三个人可派,他们各自能完成任务的概率分别,假设互不相等,且假定各人能否完成任务的事件相互独立。
(Ⅰ)如果按甲最先、乙次之、丙最后的顺序派人,求任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(Ⅱ)若按某指定顺序派人,这三个人各自能完成任务的概率依次为,其中是的一个排列,求所需派出人员数目的分布列和均值(数学期望);
(Ⅲ)假定,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数学期望)达到最小.
解不等式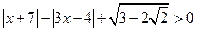
已知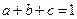 ,求证:
,求证:
已知函数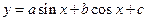 的图象上有一个最低点
的图象上有一个最低点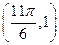 ,将图象上每个点的纵坐标不变,横坐标缩小到原来的
,将图象上每个点的纵坐标不变,横坐标缩小到原来的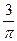 ,然后将所得图象向左平移一个单位得到
,然后将所得图象向左平移一个单位得到 的图象,若方程
的图象,若方程 的所有正根依次成为一个公差为3的等差数列,求
的所有正根依次成为一个公差为3的等差数列,求  的解析式.
的解析式.
某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度 (米)随着时间
(米)随着时间 而周期性变化,每天各时刻
而周期性变化,每天各时刻 的浪高数据的平均值如下表:
的浪高数据的平均值如下表:
 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
 |
1.0 |
1.4 |
1.0 |
0.6 |
1.0 |
1.4 |
0.9 |
0.5 |
1.0 |
试画出散点图;
观察散点图,从
 中选择一个合适的函数模型,并求出该拟合模型的解析式;
中选择一个合适的函数模型,并求出该拟合模型的解析式;如果确定在白天7时~19时当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
是否存在实数 ,使得函数
,使得函数 在闭区间
在闭区间 上的最大值是
上的最大值是 ?若存在,求出对应的
?若存在,求出对应的 值?若不存在,试说明理由.
值?若不存在,试说明理由.