(Ⅰ)设,,证明:.
(Ⅱ),证明:.
(本题满分18分,第(1)小题9分,第(2)小题9分)
设复数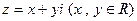 与复平面上点
与复平面上点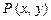 对应.
对应.
(1)设复数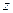 满足条件
满足条件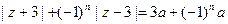 (其中
(其中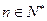 ,常数
,常数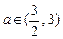 ),当
),当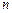 为奇数时,动点
为奇数时,动点 的轨迹为
的轨迹为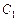 ;当
;当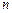 为偶数时,动点
为偶数时,动点 的轨迹为
的轨迹为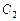 ,且两条曲线都经过点
,且两条曲线都经过点 ,求轨迹
,求轨迹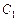 与
与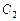 的方程;
的方程;
(2)在(1)的条件下,轨迹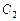 上存在点
上存在点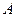 ,使点
,使点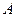 与点
与点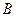
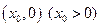 的最小距离不小于
的最小距离不小于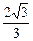 ,求实数
,求实数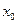 的取值范围.
的取值范围.
(本题满分16分,第(1)小题6分,第(2)小题10分)
如图,弯曲的河流是近似的抛物线 ,公路
,公路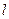 恰好是
恰好是 的准线,
的准线, 上的点
上的点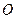 到
到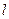 的距离最近,且为
的距离最近,且为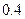 千米,城镇
千米,城镇 位于点
位于点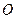 的北偏东
的北偏东 处,
处, 千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路
千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路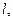 以便建立水陆交通网.
以便建立水陆交通网.
(1)建立适当的坐标系,求抛物线 的方程;
的方程;
(2)为了降低修路成本,必须使修建的两条公路总长最小,请给出修建方案(作出图形,在图中标出此时码头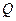 的位置),并求公路总长的最小值(精确到0.001千米)
的位置),并求公路总长的最小值(精确到0.001千米)
已知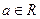 ,且以下命题都为真命题:
,且以下命题都为真命题:
命题 实系数一元二次方程
实系数一元二次方程 的两根都是虚数;
的两根都是虚数;
命题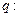 存在复数
存在复数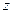 同时满足
同时满足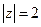 且
且 .
.
求实数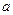 的取值范围.
的取值范围.
(本题满分12分,第(1)小题6分,第(2)小题6分)
如图,在棱长为1的正方体中,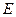 是棱
是棱 的中点,
的中点,
(1)求证: ;
;
(2)求 与平面
与平面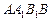 所成角大小(用反三角函数表示).
所成角大小(用反三角函数表示).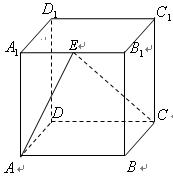
已知函数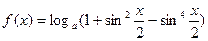 ,其中
,其中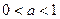 .
.
(1)判定函数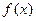 的奇偶性;
的奇偶性;
(2)函数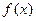 是否周期函数?若是,最小正周期是多少?
是否周期函数?若是,最小正周期是多少?
(3)试写出函数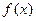 的单调区间和最大值、最小值;
的单调区间和最大值、最小值;
(4)当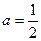 时,试研究关于
时,试研究关于 的方程
的方程 在
在 上的解的个数.
上的解的个数.