如图，直线AE、CF分别被直线EF、AC所截，已知，∠1=∠2，AB平分∠EAC，CD平分∠ACG．将下列证明AB∥CD的过程及理由填写完整．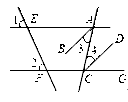
证明：∵ ∠1=∠2 （ 已知 ）
∴ AE∥ （ ）
∴ ∠EAC =∠ ，（ ）
而AB平分∠EAC，CD平分∠ACG（ 已知 ）
∴ ∠ = 
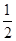∠EAC，∠4= 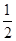∠ （ 角平分线的定义 ）
∴ ∠ =∠4（等量代换）
∴ AB∥CD（ ）．