(1)过抛物线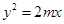 焦点F作x轴的垂线交抛物线于A、B两点,且
焦点F作x轴的垂线交抛物线于A、B两点,且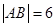 ,求m的值;
,求m的值;
(2)求焦点在直线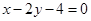 上的抛物线标准方程.
上的抛物线标准方程.
(本小题满分10分)已知曲线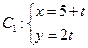 (
(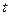 为参数),
为参数),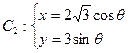 (
(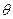 为参数),点
为参数),点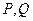 分别在曲线
分别在曲线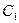 和
和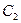 上,求线段
上,求线段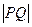 长度的最小值.
长度的最小值.
(本小题满分12分)已知函数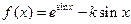 .
.
(Ⅰ)若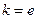 ,试确定函数
,试确定函数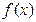 的单调递增区间;
的单调递增区间;
(Ⅱ)若对于任意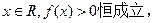 试确定实数
试确定实数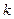 的取值范围;
的取值范围;
(Ⅲ)若函数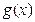 =
=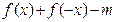 在
在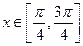 上有两个零点,求实数
上有两个零点,求实数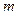 的取值范围.
的取值范围.
(本小题满分12分)在平面直角坐标系中,已知
 ,
,
 ,
, (
( ),
),
 ,O为坐标原点,若实数
,O为坐标原点,若实数 使向量
使向量 ,
, 和
和 满足:
满足: ,设点P的轨迹为
,设点P的轨迹为 .
.
(Ⅰ)求 的方程,并判断
的方程,并判断 是怎样的曲线;
是怎样的曲线;
(Ⅱ)当 时,过点
时,过点 且斜率为1的直线与
且斜率为1的直线与 相交的另一个交点为
相交的另一个交点为 ,能否在直线
,能否在直线 上找到一点
上找到一点 ,恰使
,恰使 为正三角形?请说明理由.
为正三角形?请说明理由.
(本小题满分12分)已知向量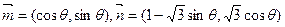 ,
,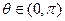 ,若
,若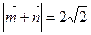 ,求
,求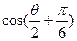 的值.
的值.
(本小题满分12分)已知函数 的最
的最 小正
小正
周期为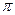 ,其
,其 图象的一条对称轴是直线
图象的一条对称轴是直线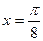 .
.
(Ⅰ)求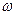 ,
, ;
;
(Ⅱ)求函数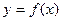 的单调递减区间;
的单调递减区间;
(Ⅲ)画出函数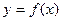 在区间
在区间 上的图象.
上的图象.