如图所示：一吊灯的下圆环直径为4m，圆心为O，通过细绳悬挂在天花板上，圆环呈水平状态，并且与天花板的距离（即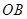
）为2m，在圆环上设置三个等分点A1，A2，A3。点C为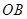上一点（不包含端点O、B），同时点C与点A1，A2，A3，B均用细绳相连接，且细绳CA1，CA2，CA3的长度相等。设细绳的总长为
，
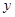（1）设∠CA1O =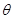
(rad)，将y表示成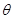的函数关系式；
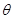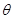（2）请你设计，当角正弦值的大小是多少时，细绳总长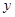最小，并指明此时 BC应为多长。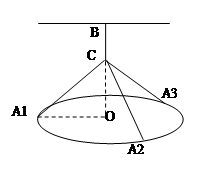
（本小题满分12分）已知抛物线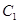
：
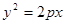的准线经过双曲线
：
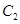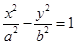的左焦点，若抛物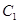线与双曲线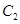的一个交点是
．
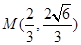（1）求抛物线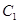的方程； （2）求双曲线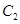的方程．
（本小题满分12分）某纺纱厂生产甲、乙两种棉纱，已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨；生产乙种棉纱需耗一级子棉1吨、二级子棉2吨，每1吨甲种棉纱的利润是600元，每1吨乙种棉纱的利润是900元，工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨．甲、乙两种棉纱应各生产多少，能使利润总额最大?
（本小题满分12分）圆经过点
和
.
（1）若圆的面积最小，求圆的方程；
（2）若圆心在直线
上，求圆的方程。
（本小题满分12分）已知直线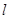
的方程为
, 求直线
的方程, 使得：
(1) 与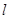平行, 且过点(－1,3) ;
(2) 与垂直, 且与两轴围成的三角形面积为4.
设双曲线C：
的左、右顶点分别为A1、A2，垂直于x轴的直线m与双曲线C交于不同的两点
。
（1）若直线m与x轴正半轴的交点为T，且
，求点T的坐标；
（2）求直线A1P与直线A2Q的交点M的轨迹E的方程；
（3）过点F（1，0）作直线l与（Ⅱ）中的轨迹E交于不同的两点A、B，设
，若
（T为（1）中的点）的取值范围。