(本小题满分14分)已知角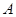 、
、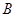 、
、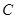 是
是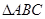 的内角,
的内角,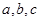 分别是其对边长,向量
分别是其对边长,向量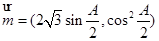 ,
,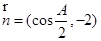 ,
,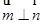 .
.
(1)求角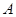 的大小;
的大小;
(2)若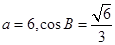 ,求
,求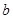 的长.
的长.
从某居民区随机抽取10个家庭,获得第 个家庭的月收入
个家庭的月收入 (单位:千元)与月储蓄
(单位:千元)与月储蓄 (单位:千元)的数据资料,算得
(单位:千元)的数据资料,算得 ,
, ,
, ,
, .
.
(1)求家庭的月储蓄 对月收入
对月收入 的线性回归方程
的线性回归方程 ;
;
(2)判断变量 与
与 之间是正相关还是负相关;
之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
其中 ,
,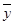 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为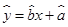
附:线性回归方程 中,
中,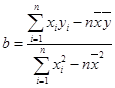 ,
, ,
,
设过原点 的直线与圆
的直线与圆 :
: 的一个交点为
的一个交点为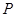 ,点
,点 为线段
为线段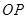 的中点。
的中点。
(1)求圆 的极坐标方程;
的极坐标方程;
(2)求点 轨迹的极坐标方程,并说明它是什么曲线.
轨迹的极坐标方程,并说明它是什么曲线.
已知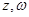 为复数,
为复数, 为纯虚数,
为纯虚数,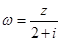 ,且
,且 ,求复数
,求复数 .
.
已知函数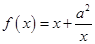 ,
,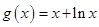 ,其中
,其中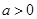 .
.
(1)若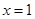 是函数
是函数 的极值点,求实数
的极值点,求实数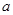 的值;
的值;
(2)若对任意的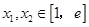 (
( 为自然对数的底数)都有
为自然对数的底数)都有 ≥
≥ 成立,求实数
成立,求实数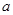 的取值范围.
的取值范围.
设函数f(x)=x2-mlnx,g(x)=x2-x+a.
(1)当a=0时,f(x)≥g(x)在(1,+∞),上恒成立,求实数m的取值范围;
(2)当m=2时,若函数h(x)=f(x)-g(x)在[1,3]上恰有两个不同的零点,求实数a的取值范围.