(本题满分10分)
已知四棱锥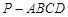 的底面为直角梯形,
的底面为直角梯形,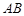 //
//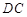 ,
,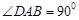 ,
,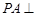 底面
底面 ,且
,且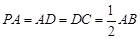 .
.
(Ⅰ)证明: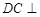 平面
平面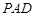 ;
;
(Ⅱ)求二面角 的余弦值的大小.
的余弦值的大小.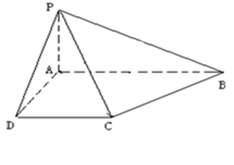
(本小题满分12分)
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作四次试验,得到的数据如下:
| 零件的个数x(个) |
2 |
3 |
4 |
5 |
| 加工的时间y(小时) |
2.5 |
3 |
4 |
4.5 |
(1)已知零件个数与加工时间线性相关,求出y关于x的线性回归方程;
(2)试预测加工10个零件需要多少时间?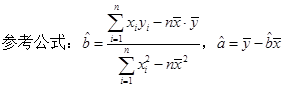
(本小题满分12分)口袋中装有除编号外其余完全相同的5个小球,编号依次为1,2,3,4,5.现从中同时取出两个球,分别记录下其编号为m,n(其中m<n).
(1)用(m,n)表示抽取结果,列出所有可能的抽取结果;
(2)求“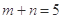 ”的概率;
”的概率;
(3)求“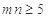 ”的概率.
”的概率.
(本小题满分12分)
如图所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以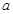 表示.已知甲、乙两个小组的数学成绩的平均分相同.
表示.已知甲、乙两个小组的数学成绩的平均分相同.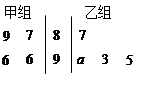
(1)求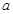 的值;
的值;
(2)求甲、乙两个小组数学成绩的方差,并说明哪个小组的成绩相对比较稳定;
参考公式: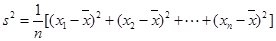
(本小题满分12分)
已知一组数据的频率分布直方图如下.求(1)众数;(2)中位数;(3)平均数.
(本小题满分10分)选修4-5:不等式选讲
已知正实数 满足:
满足: .
.
(1)求 的最小值
的最小值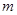 ;
;
(2)设函数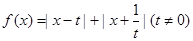 ,对于(1)中求得的
,对于(1)中求得的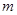 ,是否存在实数
,是否存在实数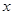 ,使得
,使得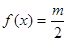 成立,说明理由.
成立,说明理由.