解答题(本题共10分.请写出文字说明, 证明过程或演算步骤):
已知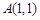 是椭圆
是椭圆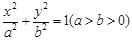 上一点,
上一点,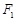 ,
,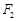 是椭圆的两焦点,且满足
是椭圆的两焦点,且满足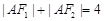
(Ⅰ)求椭圆方程;
(Ⅱ)设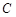 、
、 是椭圆上任两点,且直线
是椭圆上任两点,且直线 、
、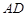 的斜率分别为
的斜率分别为 、
、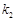 ,若存在常数
,若存在常数 使
使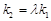 ,求直线
,求直线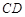 的斜率.
的斜率.
(本小题满分14分)已知函数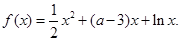
(Ⅰ)若函数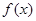 是定义域上的单调函数,求实数
是定义域上的单调函数,求实数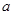 的最小值;
的最小值;
(Ⅱ)方程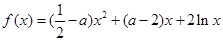 有两个不同的实数解,求实数
有两个不同的实数解,求实数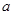 的取值范围;
的取值范围;
(Ⅲ)在函数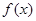 的图象上是否存在不同两点
的图象上是否存在不同两点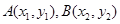 ,线段
,线段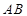 的中点的横坐标为
的中点的横坐标为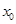 ,有
,有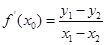 成立?若存在,请求出
成立?若存在,请求出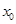 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分14分)已知函数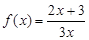 ,数列
,数列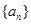 满足
满足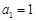 ,
,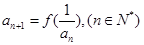 ,
,
(1)求数列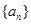 的通项公式;
的通项公式;
(2)设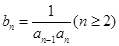 ,
,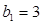 ,
,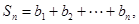 若
若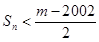 对一切
对一切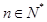 成立,求最小正整数
成立,求最小正整数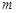 的值.
的值.
(本小题满分13分)如图,焦距为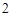 的椭圆
的椭圆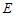 的两个顶点分别为
的两个顶点分别为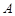 和
和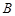 ,且
,且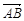 与n
与n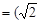 ,
,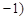 共线.
共线.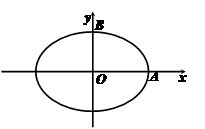
(Ⅰ)求椭圆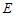 的标准方程;
的标准方程;
(Ⅱ)若直线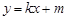 与椭圆
与椭圆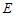 有两个不同的交点
有两个不同的交点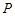 和
和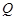 ,且原点
,且原点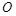 总在以
总在以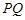 为直径的圆的内部,求实数
为直径的圆的内部,求实数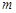 的取值范围.
的取值范围.
(本小题满分13分)如图,在四棱锥 中,底面
中,底面 是等腰梯形,
是等腰梯形,  ∥
∥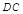 ,
, ,
,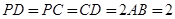 ,
,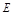 为
为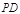 的中点.
的中点.
(Ⅰ)求证: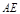 ∥平面
∥平面 ;
;
(Ⅱ)若
(ⅰ)求证平面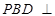 平面
平面 ;
;
(ⅱ)求直线 与底面
与底面 成角的正弦值.
成角的正弦值.
设函数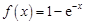 .
.
(Ⅰ)证明:当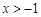 时,
时,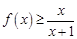 ;
;
(Ⅱ)设当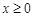 时,
时,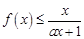 ,求实数
,求实数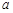 的取值范围.
的取值范围.