感知：利用图形中面积的等量关系可以得到某些数学公式．例如，根据图①甲，我们可以得到两数和的平方公式：
，根据图①乙能得到的数学公式是 ．
拓展：图②是由四个完全相同的直角三角形拼成的一个大正方形，直角三角形的两直角边长为
，
，斜边长为
，利用图②中的面积的等量关系可以得到直角三角形的三边长之间的一个重要公式，这个公式是： ，这就是著名的勾股定理．请利用图②证明勾股定理．
应用：我国古代数学家赵爽的“勾股圆方图”是由四个完全相同的直角三角形与中间的一个小正方形拼成一个大正方形（如图③所示）．如果大正方形的面积是17，小正方形的面积是1，直角三角形的两直角边长分别为
，那么
的值是 ．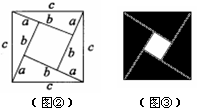
在△ABC中，AD是高，AE是角平分线.，∠B=20°，∠C=60，求∠CAD和∠DAE的度数.
如图，AB∥DC，∠ABC=∠ADC，问：AE与FC平行吗？请说明理由.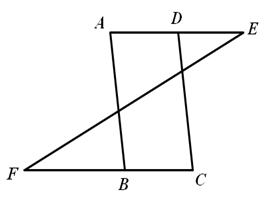
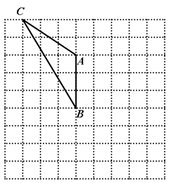
如图，△ABC的顶点都在方格纸的格点上，将△ABC向下平移3格，再向右平移4格.请在图中画出平移后的△A′B′C′
在图中画出△A′B′C′的高C′D′
观察下列等式：
①
；②
；
③
；④
；
……猜想并写出第
个算式：；请说明你写出的等式的正确性．
把上述
个算式的两边分别相加，会得到下面的求和公式吗？请写出具体的推导过程．
．我们规定：分子是1，分母是正整数的分数叫做单位分数．任意一个真分数都可以表示成不同的单位分数的和的形式，且有无数多种表示方法．根据上面得出的两个结论，请将真分数
表示成不同的单位分数的和的形式．（写出一种即可）
某企业为了改善污水处理条件，决定购买A、B两种型号的污水处理设备共8台，其中每台的价格、月处理污水量如下表：
| A型 |
B型 |
|
| 价格(万元/台) |
8 |
6 |
| 月处理污水量(吨/月) |
200 |
180 |
经预算，企业最多支出57万元购买污水处理设备，且要求设备月处理污水量不低于1490吨．企业有哪几种购买方案？
哪种购买方案更省钱？