已知圆锥曲线C:
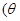 为参数)和定点
为参数)和定点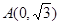 ,
,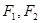 是此圆锥曲线的左、右焦点。
是此圆锥曲线的左、右焦点。
(1)以原点O为极点,以x轴的正半轴为极轴建立极坐标系,求直线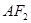 的极坐标方程;
的极坐标方程;
(2)经过点 ,且与直线
,且与直线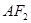 垂直的直线
垂直的直线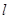 交此圆锥曲线于
交此圆锥曲线于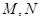 两点,求
两点,求 的值.
的值.
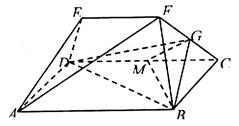
(本小题满分14分)如图几何体中,四边形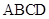 为矩形,
为矩形,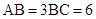 ,
,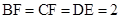 ,
,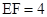 ,
,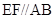 ,
,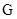 为
为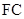 的中点,
的中点,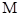 为线段
为线段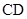 上的一点,且
上的一点,且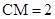 .
.
(1)证明: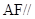 平面
平面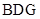 ;
;
(2)证明:平面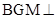 平面
平面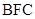 ;
;
(3)求三棱锥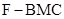 的体积
的体积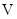 .
.
(本小题满分12分)某次的一次学科测试成绩的茎叶图和频率分布直方图都受到不同程度的
污损,可见部分如图.
(1)求参加测试的总人数及分数在 之间的人数;
之间的人数;
(2)若要从分数在 之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,恰有一份分
之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,恰有一份分
数在 之间的概率.
之间的概率.
【原创】(本小题满分12分)已知向量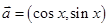 ,
,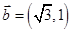 ,设函数
,设函数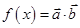 .
.
(1)求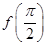 的值;
的值;
(2)若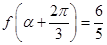 ,
,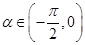 ,求
,求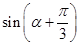 的值.
的值.
(本小题满分14分)已知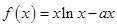 ,
,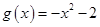 .
.
(1)当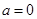 时,求函数
时,求函数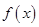 的单调区间;
的单调区间;
(2)对一切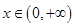 ,
,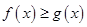 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知椭圆 的中心在原点
的中心在原点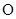 ,焦点在
,焦点在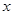 轴上,离心率为
轴上,离心率为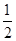 ,右焦点到右
,右焦点到右
顶点的距离为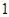 .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)是否存在与椭圆 交于
交于 ,
,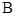 两点的直线
两点的直线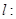
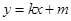 (
( ),使得
),使得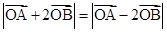
成立?若存在,求出实数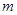 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.