（本小题满分12分）袋中装着标有数字1，2，3，4，5的小球各2个，从袋中任取3个小球，按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，用
表示取出的3个小球上的最大数字，求：
（Ⅰ）取出的3个小球上的数字互不相同的概率；
（Ⅱ）随机变量的分布列和数学期望；
（Ⅲ）计分介于20分到40分之间的概率
设函数f(x)＝ln x＋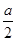
x2－(a＋1)x(a>0，a为常数)．
(1)讨论f(x)的单调性；
(2)若a＝1，证明：当x>1时，f(x)< 
x2－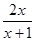
－
.
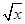(13分)某工厂某种产品的年固定成本为250万元，每生产x千件，需另投入成本C(x)，当年产量不足80千件时，C(x)＝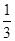
x2＋10x(万元)；当年产量不小于80千件时，C(x)＝51x＋
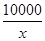－1 450(万元)．每件商品售价为0.05万元．通过市场分析，该厂生产的商品能全部售完．
(1)写出年利润L(x)(万元)关于年产量x(千件)的函数解析式；
(2)年产量为多少千件时，该厂在这一商品的生产中所获利润最大？
如图1所示，在Rt△ABC中，AC＝6，BC＝3，∠ABC＝90°，CD为∠ACB的平分线，点E在线段AC上，CE＝4.如图2所示，将△BCD沿CD折起，使得平面BCD⊥平面ACD，连接AB，设点F是AB的中点．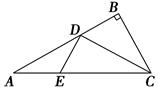
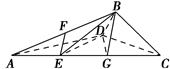
图1图2
(1)求证：DE⊥平面BCD；
(2)若EF∥平面BDG，其中G为直线AC与平面BDG的交点，求三棱锥BDEG的体积．
如图，在三棱柱ABCA1B1C1中，底面△ABC是等边三角形，D为AB中点．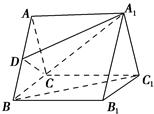
(1)求证：BC1∥平面A1CD；
(2)若四边形BCC1B1是矩形，且CD⊥DA1，求证：三棱柱ABCA1B1C1是正三棱柱．
如图，在边长为4的菱形ABCD中，∠DAB＝60°，点E、F分别在边CD、CB上，点E与点C、D不重合，EF⊥AC，EF∩AC＝O，沿EF将△CEF翻折到△PEF的位置，使平面PEF⊥平面ABFED.
(1)求证：BD⊥平面POA；
(2)记三棱锥PABD体积为V1，四棱锥PBDEF体积为V2，且
，求此时线段PO的长．