(本小题满分12分)已知 的三边长
的三边长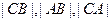 成等差数列,若点
成等差数列,若点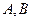 的坐标分别为
的坐标分别为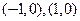 .(1)求顶点
.(1)求顶点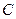 的轨迹
的轨迹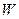 的方程;(2)若线段
的方程;(2)若线段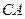 的延长线交轨迹
的延长线交轨迹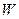 于点
于点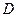 ,当
,当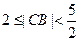 时求线段
时求线段 的垂直平分线
的垂直平分线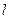 与
与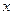 轴交点的横坐标的取值范围.
轴交点的横坐标的取值范围.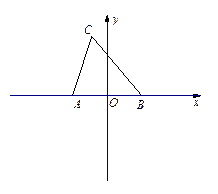
已知函数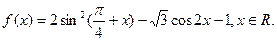
 1)若函数
1)若函数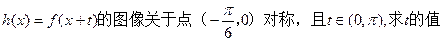 ;
;
(2)设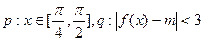 ,若p是q的充分条件,求实数m的取值范围.
,若p是q的充分条件,求实数m的取值范围.

(本小题满分12分) 已知直四棱柱ABCD—A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1
已知直四棱柱ABCD—A1B1C1D1的底面是菱形,且∠DAB=60°,AD=AA1,F为棱BB1
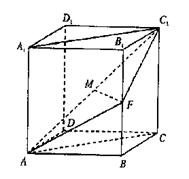 的中点,M为线段AC1的中点.
的中点,M为线段AC1的中点.
(1)求证:直线MF∥平面ABCD;
(2)求证:平面AFC1⊥平面ACC1A1;
(3)求平面AFC1与与平面ABCD所成二面角的大小.

(本小题满分12分) 学网某种家用电器每台的销售利润与该电器的无故障使用时间
学网某种家用电器每台的销售利润与该电器的无故障使用时间 (单位:年)有关. 若
(单位:年)有关. 若 ,则销售利润为
,则销售利润为 元;若
元;若 ,则销售利润为
,则销售利润为 元;若
元;若 ,则销售利润为
,则销售利润为 元.设每台该种电器的无故障使用时间
元.设每台该种电器的无故障使用时间 ,
, 及
及 这三种情况发生的概率分别为
这三种情况发生的概率分别为 ,
, ,
, ,叉知
,叉知 ,
, 是方程
是方程 的两个根,且
的两个根,且 (1)求
(1)求 ,
, ,
, 的值;(2)记
的值;(2)记 表示销售两台这种家用电器的销售利润总和,求
表示销售两台这种家用电器的销售利润总和,求 的期望.
的期望.
(本小题满分12分) 已知向量
已知向量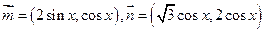 ,定义函数
,定义函数
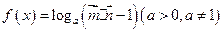 ,求函数
,求函数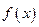 的最小正周期、单调递增区间.
的最小正周期、单调递增区间.