如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.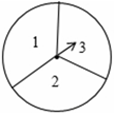
(1)转动转盘一次,转到数字是3的区域的概率是多少?
(2)转动转盘两次,用画树状图或列表的方法求两次指针所指区域数字不同的概率;
(3)在第(2)题中,两次转到的区域的数字作为两条线段的长度,如果第三条线段的长度为5,求这三条线段能构成三角形的概率.
如图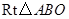 中,
中,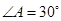 ,
,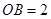 ,如果将
,如果将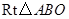 在坐标平面内,绕原点
在坐标平面内,绕原点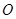 按顺时针方向旋转到
按顺时针方向旋转到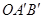 的位置.
的位置.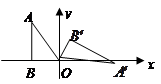
(1)求点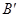 的坐标.
的坐标.
(2)求顶点 从开始到
从开始到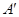 点结束经过的路径长.
点结束经过的路径长.
“五·一”期间,某书城为了吸引读者,设立了一个可以自由转动的转盘(如图,转盘被平均分成12份),并规定:读者每购买100元的书,就可获得一次转动转盘的机会,如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么读者就可以分别获得45元、30元、25元的购书券,凭购书券可以在书城继续购书.如果读者不愿意转转盘,那么可以直接获得10元的购书券.转转盘和直接获得购书券,你认为哪种方式对读者更合算?请说明理由. 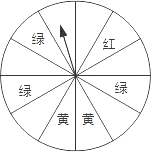
(1)计算:
(2)A、B两人共解方程组 ,由于A看错了方程(1)中的a,得到的解是
,由于A看错了方程(1)中的a,得到的解是 ,而B看错了方程(2)中的b, 得到的解是
,而B看错了方程(2)中的b, 得到的解是 ,试求
,试求 的值.
的值.
如图所示,在平面直角坐标系xOy中,矩形OABC的边长OA、OC分别为12cm、6cm,点A、C分别在y轴的负半轴和x轴的正半轴上,抛物线y=ax2+bx+c经过点A、B,且18a+c=0.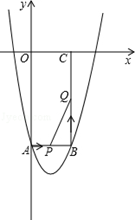
(1)求抛物线的解析式.
(2)如果点P由点A开始沿AB边以1cm/s的速度向终点B移动,同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动.
①移动开始后第t秒时,设△PBQ的面积为S,试写出S与t之间的函数关系式,并写出t的取值范围.
②当S取得最大值时,在抛物线上是否存在点R,使得以P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
如图,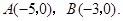 点
点 在
在 轴的正半轴上,
轴的正半轴上, ,
,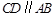 ,
,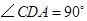 .点
.点 从点
从点 出发,沿
出发,沿 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为 秒.
秒.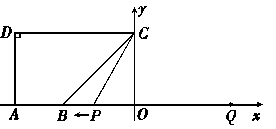
(1)求点 的坐标;
的坐标;
(2)当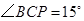 时,求
时,求 的值;
的值;
(3)以点 为圆心,
为圆心,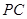 为半径的
为半径的 随点
随点 的运动而变化,当
的运动而变化,当 与四边形
与四边形 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求 的值.
的值.