如图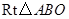 中,
中, ,
, ,如果将
,如果将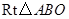 在坐标平面内,绕原点
在坐标平面内,绕原点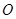 按顺时针方向旋转到
按顺时针方向旋转到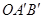 的位置.
的位置.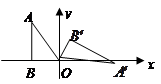
(1)求点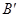 的坐标.
的坐标.
(2)求顶点 从开始到
从开始到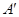 点结束经过的路径长.
点结束经过的路径长.
如图,已知二次函数的图象与 轴交于 和 两点,与 轴交于 ,对称轴为直线 ,直线 经过点 ,且与 轴交于点 ,与抛物线交于点 ,与对称轴交于点 .
(1)求抛物线的解析式和 的值;
(2)在 轴上是否存在点 ,使得以 为顶点的三角形与 相似,若存在,求出点 的坐标;若不存在,试说明理由;
(3)直线 上有 两点 在 的左侧 ,且 ,若将线段 在直线 上平移,当它移动到某一位置时,四边形 的周长会达到最小,请求出周长的最小值(结果保留根号).

在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“连杆”,推动“连杆”带动磨盘转动,将粮食磨碎,物理学上称这种动力传输工具为“曲线连杆机构”.
小明受此启发设计了一个“双连杆机构”,设计图如图①,两个固定长度的“连杆” 的连接点 在 上,当点 在 上转动时,带动点 分别在射线 上滑动, .当 与 相切时,点 恰好落在 上,如图②.请仅就图②的情形解答下列问题.
(1)求证: ;
(2)若 的半径为 ,求 的长.

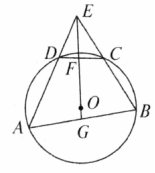
如图,已知 是四边形 的外接圆,直线 相交于点 是弦 的中点,延长直线 交弦 于点 ,求证:
(1) ;
(2) .
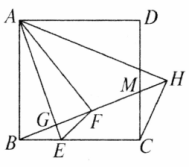
如图,已知正方形 ,点 是 边上一点,将 沿直线 折叠,点 落在 处,连接 并延长,与 的平分线相交于点 ,与 分别相交于点 , ,连接 .
(1)求证:
(2)若 ,求点 到直线 的距离;
(3)当点 在 边上(端点除外)运动时, 的大小是否变化?为什么?
如图所示,在 中, 为 边上一点, 是方程 的一个较大的根,求 的长
