欲测河的宽度,在一岸边选定A、B两点,望对岸的标记物C,测得∠CAB=45°,∠CBA=75°,AB=120 m,求河宽.(精确到0.01 m)
(本小题满分14分)
长方体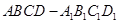 中,
中, ,
,  ,
, 是底面对角线的交点。
是底面对角线的交点。
(Ⅰ)求证: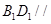 平面
平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求三棱锥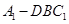 的体积。
的体积。
(本小题满分12分)
某人有3枚钥匙,其中只有一枚房门钥匙,但忘记了开房门的是哪一枚,于是,他逐枚不重复地试开,问:
(Ⅰ)恰好第三次打开房门锁的概率是多少?
(Ⅱ)两次内打开房门的概率是多少?
(本小题满分12分)
已知 ,且
,且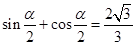 .
.
(Ⅰ)求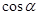 的值;
的值;
(Ⅱ)若 ,
, ,求
,求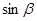 的值.[来源
的值.[来源
(本小题满分14分)
设函数 .
.
(1)若函数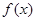 在区间(-2,0)内恰有两个零点,求a的取值范围;
在区间(-2,0)内恰有两个零点,求a的取值范围;
(2)当a=1时,求函数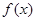 在区间[t,t+3]上的最大值.
在区间[t,t+3]上的最大值.
(本小题满分14分)
设双曲线C: (a>0,b>0)的一个焦点坐标为(
(a>0,b>0)的一个焦点坐标为(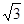 ,0),离心率
,0),离心率 , A、B是双曲线上的两点,AB的中点M(1,2).
, A、B是双曲线上的两点,AB的中点M(1,2).
(1)求双曲线C的方程;
(2)求直线AB方程;
(3)如果线段AB的垂直平分线与双曲线交于C、D两点,那么A、B、C、D四点是否共圆?为什么?