已知,如图,MN⊥AB,垂足为G,MN⊥CD,垂足为H,直线EF分别交AB、CD于G、Q,∠GQC=120°,求∠EGB和∠HGQ的度数。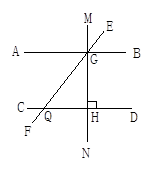
某超市为庆祝开业举办大酬宾抽奖活动,凡在开业当天进店购物的顾客,都能获得一次抽奖的机会,抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和,若两次所得的数字之和为8,则可获得50元代金券一张;若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张;其他情况都不中奖.
(1)请用列表或树状图(树状图也称树形图)的方法(选其中一种即可),把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率 .
如图, 为 的直径, 是 上一点,过点 的直线交 的延长线于点 , ,垂足为 , 是 与 的交点, 平分 .
(1)求证: 是 的切线;
(2)若 , ,求图中阴影部分的面积.

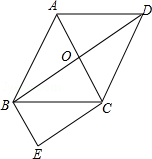
如图,菱形 的对角线 与 交于点 , , , .
(1)求 的值;
(2)求证:四边形 是矩形.
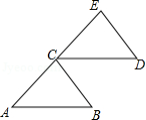
如图:点 是 的中点, , ,求证: .
如图,在 中, , 是 边上的一点,以 为半径的 与边 相切于点 .
(1)若 , ,求 的半径;
(2)过点 作弦 于 ,连接 ,若 ,求证:四边形 是菱形.
