设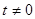 ,点P(
,点P(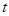 ,0)是函数
,0)是函数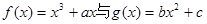 的图象的一个公共点,两函数的图象在点P处有相同的切线.
的图象的一个公共点,两函数的图象在点P处有相同的切线.
(Ⅰ)用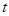 表示a,b,c;
表示a,b,c;
(Ⅱ)若函数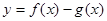 在(-1,3)上单调递减,求
在(-1,3)上单调递减,求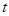 的取值范围.
的取值范围.
正项数列 中,前n项和为
中,前n项和为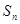 ,且
,且 ,且
,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设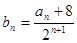 ,
, ,证明
,证明 .
.
设数列{ }是等差数列,
}是等差数列,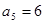 ,
, 时,若自然数
时,若自然数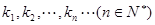 满足
满足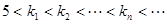 ,使得
,使得 成等比数列,(1)求数列{
成等比数列,(1)求数列{ }的通项公式;(2)求数列
}的通项公式;(2)求数列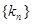 的通项公式及其前n项的和
的通项公式及其前n项的和
设 是三角形的内角,且
是三角形的内角,且 和
和 是关于
是关于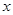 方程
方程 的两个根.
的两个根.
(1)求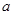 的值;
的值;
(2)求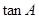 的值.
的值.
已知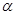 为第三象限角,
为第三象限角, .
.
(1)化简
(2)若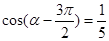 ,求
,求 的值.
的值.
设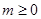 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量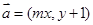 ,向量
,向量 ,
,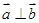 ,动点
,动点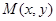 的轨迹为E.
的轨迹为E.
(1)求轨迹E的方程,并说明该方程所表示曲线的形状;
(2)已知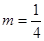 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;
(3)已知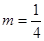 ,设直线
,设直线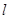 与圆C:
与圆C: (1<R<2)相切于A1,且
(1<R<2)相切于A1,且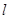 与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.
与轨迹E只有一个公共点B1,当R为何值时,|A1B1|取得最大值?并求最大值.