已知第一个正方体纸盒的棱长为6cm,第二个正方体纸盒的体积比第一个纸盒的体积大127cm3,求第二个纸盒的棱长.
解不等式:(1) 8x+1<6x-3(2)解不等式:5x-9<3(x+1)
(3) (4)
(4)
实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等. 如图1,一束光线m射到平面镜a上,被a反射后的光线为n,则入射光线m、反射光线n与平面镜a所夹的锐角∠1=∠2.
(1) 如图2,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=50°,则∠2=_____°,∠3=_____°. 
(2) 在(1)中m∥n,若∠1=55°,则∠3=______°;若∠1=40°,则∠3=______°.
(3) 由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=______°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?
探究与发现:
(1)探究一:三角形的一个内角与另两个内角的平分线所夹的角之间的关系
已知:如图1,在△ADC中,DP、CP分别平分∠ADC和∠ACD,
试探究∠P与∠A的数量关系,并说明理由.


图1图2图3
(2)探究二:四边形的两个个内角与另两个内角的平分线所夹的角之间的关系
已知:如图2,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试探究∠P与∠A+∠B的数量关系,并说明理由.
(3)探究三:六边形的四个内角与另两个内角的平分线所夹的角之间的关系
已知:如图3,在六边形ABCDEF中,DP、CP分别平分∠EDC和∠BCD,请直接写出∠P与∠A+∠B+∠E+∠F的数量关系:__ __ __.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.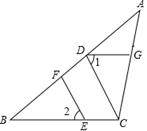
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,那么DG∥BC吗?为什么?
如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°。
(1)求∠C的度数;
(2)求∠BED的度数.