求证: 能被
能被 整除(其中
整除(其中 ).
).
某人沿一条折线段组成的小路前进,从 到
到 ,方位角(从正北方向顺时针转到
,方位角(从正北方向顺时针转到 方向所成的角)是
方向所成的角)是 ,距离是3km;从
,距离是3km;从 到
到 ,方位角是110°,距离是3km;从
,方位角是110°,距离是3km;从 到
到 ,方位角是140°,距离是(
,方位角是140°,距离是( )km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
)km.试画出大致示意图,并计算出从A到D的方位角和距离(结果保留根号).
已知函数 ,
, ,
, .
.
(1)若 ,试判断并用定义证明函数
,试判断并用定义证明函数 的单调性;
的单调性;
(2)当 时,求函数
时,求函数 的最大值的表达式
的最大值的表达式 .
.
如图,在直三棱柱 中,
中,  ,
,  ,
, ,点
,点 是
是 的中点.四面体
的中点.四面体 的体积是
的体积是 ,求异面直线
,求异面直线 与
与 所成的角.
所成的角.
若函数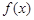 满足:集合
满足:集合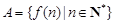 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数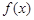 是等比源函数.
是等比源函数.
(1)判断下列函数:①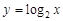 ;②
;②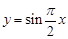 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(2)证明:对任意的正奇数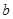 ,函数
,函数 不是等比源函数;
不是等比源函数;
(3)证明:任意的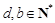 ,函数
,函数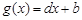 都是等比源函数.
都是等比源函数.
如图,已知平面内一动点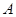 到两个定点
到两个定点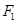 、
、 的距离之和为
的距离之和为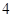 ,线段
,线段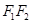 的长为
的长为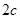
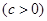 .
.
(1)求动点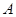 的轨迹
的轨迹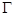 ;
;
(2)当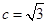 时,过点
时,过点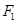 作直线
作直线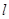 与轨迹
与轨迹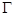 交于
交于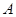 、
、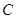 两点,且点
两点,且点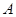 在线段
在线段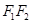 的上方,线段
的上方,线段 的垂直平分线为
的垂直平分线为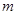
①求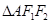 的面积的最大值;
的面积的最大值;
②轨迹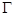 上是否存在除
上是否存在除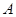 、
、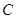 外的两点
外的两点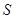 、
、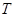 关于直线
关于直线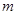 对称,请说明理由.
对称,请说明理由.