(本小题满分14分)
在四棱锥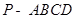 中,底面
中,底面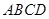 是直角梯形,
是直角梯形,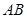 ∥
∥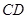 ,
,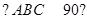 ,
,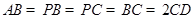 ,平面
,平面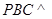 平面
平面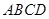 .
.
(Ⅰ)求证: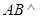 平面
平面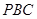 ;
;
(Ⅱ)求平面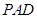 和平面
和平面 所成二面角(小于
所成二面角(小于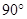 )的大小;
)的大小;
(Ⅲ)在棱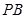 上是否存在点
上是否存在点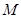 使得
使得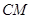 ∥平面
∥平面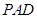 ?若
?若 存在,求
存在,求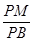 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 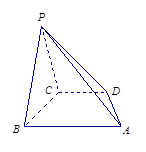
(本小题满分12分)已知函数
(1)求函数 的最大值;
的最大值;
(2)当 时,求证
时,求证 ;
;
(本小题满分12分)
已知适合不等式 的x的最大值为3,求p的值。
的x的最大值为3,求p的值。
(本小题满分12分)如图,在四棱锥P—ABCD中,底面 ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点.
ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点.
(1)求直线AC与PB所成角的余弦值;
(2)在侧面PAB内找一点N,使NE⊥面PAC,并求出N点到AB和AP的距离.
(本小题满分12分)
用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长 方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
已知数列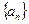 是首项
是首项 公比
公比 的等比数列,设
的等比数列,设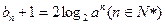 ,数列
,数列 满足
满足 .
.
(1)求证: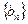 是等差数列;
是等差数列;
(2)求数列 的前n项和Sn;
的前n项和Sn;
(3)若 对一切正整数
对一切正整数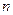 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。