(本题12分)为了研究化肥对小麦产量的影响,某科学家将一片土地划分成200个 的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
的小块,并在100个小块上施用新化肥,留下100个条件大体相当的小块不施用新化肥.下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表(小麦产量单位:kg)
表1:施用新化肥小麦产量频数分布表
| 小麦产量 |
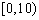 |
 |
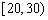 |
 |
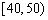 |
| 频数 |
10 |
35 |
40 |
10 |
5 |
表2:不施用新化肥小麦产量频数分布表
| 小麦产量 |
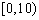 |
 |
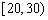 |
 |
| 频数 |
15 |
50 |
30 |
5 |
(10) 完成下面频率分布直方图;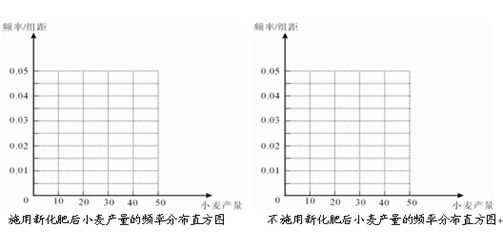
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量;
(3)完成下面2×2列联表,并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3:
| |
小麦产量小于20kg |
小麦产量不小于20kg |
合计 |
| 施用新化肥 |
 |
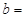 |
|
| 不施用新化肥 |
 |
 |
|
| 合计 |
|
|
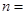 |
附: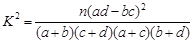
 |
0.050 |
0.010 |
0.005 |
0.001 |
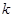 |
3.841 |
6.635 |
7.879 |
10.828 |
在平面直角坐标系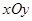 中,角
中,角 的终边经过点
的终边经过点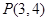 .
.
(1)求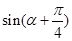 的值;
的值;
(2)若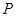 关于
关于 轴的对称点为
轴的对称点为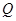 ,求
,求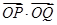 的值.
的值.
已知数列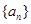 中
中
 .
.
(1)是否存在实数 ,使数列
,使数列 是等比数列?若存在,求
是等比数列?若存在,求 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(2)若 是数列
是数列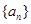 的前
的前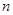 项和,求满足
项和,求满足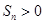 的所有正整数
的所有正整数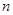 .
.
已知函数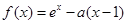 ,其中
,其中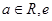 为自然对数底数.
为自然对数底数.
(1)当 时,求函数
时,求函数 在点
在点 处的切线方程;
处的切线方程;
(2)讨论函数 的单调性,并写出相应的单调区间;
的单调性,并写出相应的单调区间;
(3)已知 ,若函数
,若函数 对任意
对任意 都成立,求
都成立,求 的最大值.
的最大值.
如图,已知椭圆 ,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在
,点B是其下顶点,过点B的直线交椭圆C于另一点A(A点在 轴下方),且线段AB的中点E在直线
轴下方),且线段AB的中点E在直线 上.
上.
(1)求直线AB的方程;
(2)若点P为椭圆C上异于A、B的动点,且直线AP,BP分别交直线 于点M、N,证明:OM·ON为定值.
于点M、N,证明:OM·ON为定值.
如图,某生态园将一三角形地块ABC的一角APQ开辟为水果园种植桃树,已知角A为 的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
(1)若围墙AP,AQ总长度为200米,如何围可使得三角形地块APQ的面积最大?
(2)已知AP段围墙高1米,AQ段围墙高1.5米,造价均为每平方米100元.若围围墙用了20000元,问如何围可使竹篱笆用料最省?