如图①，在正方形ABCD中，E是AD的中点，F是BA延长线上的一点，AF=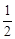
AB，
（1）求证：△ABE≌△ADF.
（2）阅读下列材料：如图②，把△ABC沿直线平移线段BC的长度，可以变到△ECD的位置；如图③，以BC为轴把△ABC翻折180°，可以变到△DBC的位置；如图④，以点A为中心，把△ABC旋转180°，可以变到△AED的位置，像这样其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状大小的图形变换，叫做三角形的全等变换.
图① 图② 图③ 图④
请回答下列问题：
（1）在图①中，可以通过平移、翻折、旋转中的哪一种方法，使△ABE变到△ADF的位置？
（2）指出图①中线段BE与DF之间的关系.
把一边长为40cm的正方形硬纸板，进行适当的剪裁，折成一个长方形盒子（纸板的厚度忽略不计）。
（1）如图1，若在正方形硬纸板的四角各剪一个同样大小的正方形，将剩余部分折成一个无盖的长方形盒子。
①要使折成的长方形盒子的底面积为484cm2，那么剪掉的正方形的边长为多少？
②折成的长方形盒子的侧面积是否有最大值？如果有，求出这个最大值及此时剪掉的正方形的边长；如果没有，请说明理由。
（2）如图2在正方形硬纸板上剪掉一些矩形（图2中阴影为剪去部分），将剩余部分折成一个有盖的长方形盒子，若折成的一个长方形盒子的表面积为550cm2，求此时长方形盒子的长、宽、高。
如图，已知△ABC中，∠C＝90º，D是AB上一点，DE⊥CD于D，交BC于E，且有AC＝AD＝CE。求证：
（1）∠ACD＝∠CED
（2）DE＝
CD
已知关于
的一元二次方程
有两个实数根，若
为正整数。
（1）求的值；
（2）求这个方程的根。
用反证法证明“三角形三个内角中，至少有一个内角小于或等于60º”。
已知：∠A，∠B，∠C是△ABC的内角。
求证：∠A，∠B，∠C中至少有一个小于或等于60º。
证明：假设求证的结论不成立，即
∴∠A＋∠B＋∠C＞
这与三角形 相矛盾。
∴假设不成立
∴
为增强学生的身体素质，学校规定学生平均每天参加户外活动的时间不少于1小时。为了解学生参加户外活动的情况，对部分学生参加户外活动的时间进行抽样调查，并将调查结果绘制作成如下两幅未画完整的统计图，请你根据图中提供的信息解答下列问题：
（1）在这次调查中共调查了多少名学生？
（2）求户外活动时间为1.5小时的人数，并补充频数分布直方图；
（3）本次调查中学生参加户外活动的平均时间是否符合学校规定？