为增强学生的身体素质,学校规定学生平均每天参加户外活动的时间不少于1小时。为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅未画完整的统计图,请你根据图中提供的信息解答下列问题:

(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)本次调查中学生参加户外活动的平均时间是否符合学校规定?
如图,点D在BC上,DE垂直平分AC,垂足为E,F是BA的中点.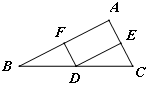
求证:DF是AB的垂直平分线.
结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示-3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于 .如果表示数a和-2的两点之间的距离是3,那么a= ;
.如果表示数a和-2的两点之间的距离是3,那么a= ;
(2)若数轴上表示数a的点位于-4与2之间,求 +
+ 的值;
的值;
(3)当a取何值时, +
+ +
+ 的值最小,最小值是多少?请说明理由.
的值最小,最小值是多少?请说明理由.
有一批水果,包装质量为每筐25千克,现抽取8筐样品进行检测,结果称重如下(单位:千克):27,24,23,28,21,26,22,27,为了求得8筐样品的总质量,我们可以选取的一个恰当的基准数进行简化运算.
(1)你认为选取的一个恰当的基准数为 ;
(2)根据你选取的基准数,用正、负数填写上表;
| 原质量 |
27 |
24 |
23 |
28 |
21 |
26 |
22 |
27 |
| 与基准数的差距 |
(3)这8筐水果的总质量是多少?
出租车司机小傅某天下午营运全是在东西走向的大道上行驶的.若如果规定向东为正,则行车里程(单位:km)如下:
+11,-2,+3,+10,-11,+5,-15,-8
(1)当把最后一名乘客送到目的地时,小傅距离出车地点的距离为多少?
(2)若每千米的营运额为7元,成本为1.5元/km,则这天下午他盈利多少元?
化简并求值:2(2a-3b)-(3a+2b+1),其中a=2,b=- .
.