如图所示，在直角坐标系的原点O 处有一放射源，向四周均匀发射速度大小相等、方向都平行于纸面的带电粒子。在放射源右侧有一很薄的挡板，垂直于x 轴放置，挡板与xoy 平面交线的两端M、N 正好与原点O 构成等边三角形，O′ 为挡板与x 轴的交点。在整个空间中，有垂直于xoy 平面向外的匀强磁场（图中未画出），带电粒子在磁场中沿顺时针方向做匀速圆周运动。已知带电粒子的质量为m，带电荷量大小为q，速度大小为υ，MN 的长度为L。（不计带电粒子的重力及粒子间的相互作用）
（1）确定带电粒子的电性；
（2）要使带电粒子不打在挡板上，求磁感应强度的最小值；
（3）要使MN 的右侧都有粒子打到，求磁感应强度的最大值。（计算过程中，要求画出各临界状态的轨迹图）
电站通过升压器、输电线和降压器把电能输送给生产和照明组成的用户，若发电机发电功率为1.2×105 W，输出电压是240 V，升压器原副线圈的匝数之比为1∶25，输电线的总电阻为10 Ω，用户需要电压为220 V．求：
(1)输电线上损失的电功率为多少？
(2)降压变压器的匝数比为多少？
如图所示，一轻质弹簧两端连着物体A和B，放在光滑的水平面上，物体A被水平速度为v0的子弹射中并且嵌入其中。已知物体B的质量为m，物体A的质量是物体B的质量的
，子弹的质量是物体B的质量的
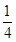，求
①弹簧压缩到最短时物体B的速度。
②弹簧的最大弹性势能。
如图所示，为玻璃材料制成的一棱镜的截面图 其中，弧AB为四分之一圆弧，O为圆心，OBCD部分为矩形。一细光束从圆弧AB的中点E沿半径射入棱镜后，恰好在O点发生全反射，经CD面反射，再从圆弧上的F点射出，已知OA=a，OD=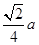
，
真空中光速为c。求
①出射光线与法线夹角的正弦值。
②光在棱镜中传播的时间。
如图所示为一下粗上细且上端开口的薄壁玻璃管，管内用水银封闭一定质量的理想气体，上管足够长。图中大小截面积分别为S1=2cm2、S2=lcm2。粗细管内水银柱长度h1=h2=2cm，封闭气体长度L=22cm。大气压强P0=76cmHg，气体初始温度为57℃。求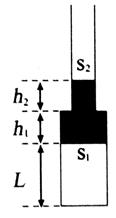
①若缓慢升高气体温度，升高至多少开尔文方可将所有水银全部挤入细管内。
②若温度升高至492K，液柱下端离开玻璃管底部的距离。
如图所示的xOy坐标系中，Y轴右侧空间存在范围足够大的匀强磁场，磁感应强度大小为B，方向垂直于xOy平面向外。Ql、Q2两点的坐标分别为(0，L)、(0，-L)，坐标为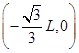
处的C点固定一平行于y轴放置的绝缘弹性挡板，C为挡板中点。带电粒子与弹性绝缘挡板碰撞前后，沿y轴方向分速度不变，沿x轴方向分速度反向，大小不变。现有质量为m，电量为+q的粒子，在P点沿PQl方向进入磁场，
，不计粒子重力。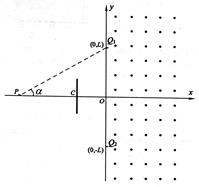
(1)若粒子从点Ql直接通过点Q2，求粒子初速度大小。
(2)若粒子从点Ql直接通过点O，求粒子第一次经过x轴的交点坐标。
(3)若粒子与挡板碰撞两次并能回到P点，求粒子初速度大小及挡板的最小长度。