如图所示为某一仪器的部分原理示意图,虚线OA、OB关于y轴对称,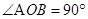 , OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求:
, OA、OB将xOy平面分为Ⅰ、Ⅱ、Ⅲ三个区域,区域Ⅰ、Ⅲ内存在水平方向的匀强电场,电场强度大小相等、方向相反。质量为m电荷量为q的带电粒子自x轴上的粒子源P处以速度v0沿y轴正方向射出,经一定时间到达OA上的M点,且此时速度与OA垂直。已知M到原点O的距离OM = L,不计粒子的重力。求:
(1)匀强电场的电场强度E的大小;
(2)为使粒子能从M点经Ⅱ区域通过OB上的N点,M、N点关于y轴对称,可在区域Ⅱ内适当范围加一垂直xOy平面的匀强磁场,求该磁场的磁感应强度的最小值和粒子经过区域Ⅲ到达x轴上Q点的横坐标;
(3)当匀强磁场的磁感应强度取(2)问中的最小值时,且该磁场仅分布在一个圆形区域内。由于某种原因的影响,粒子经过M点时的速度并不严格与OA垂直,成散射状,散射角为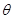 (
(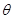 较小),但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
较小),但速度大小均相同,如图所示,求所有粒子经过OB时的区域长度。
两根足够长的光滑金属导轨平行固定在倾角为θ的斜面上,它们的间距为d.磁感应强度为B的匀强磁场充满整个空间、方向垂直于斜面向上.两根金属杆ab、cd的质量分别为m和2m,垂直于导轨水平放置在导轨上,如图所示.设杆和导轨形成的回路总电阻为R而且保持不变,重力加速度为g.
(1)给ab杆一个方向沿斜面向上的初速度,同时对ab杆施加一平行于导轨方向的恒定拉力,结果cd杆恰好保持静止而ab杆则保持匀速运动.求拉力做功的功率.
(2)若作用在ab杆的拉力与第(1)问相同,但两根杆都是同时从静止开始运动,求两根杆达到稳定状态时的速度.
如图所示,圆管构成的半圆形轨道竖直固定在水平地面上,轨道半径为R,MN为直径且与水平面垂直,直径略小于圆管内径的小球A以某一速度冲进轨道,到达半圆轨道最高点M时与静止于该处的质量与A相同的小球B发生碰撞,碰后两球粘在一起飞出轨道,落地点距N为2 R。重力加速度为g,忽略圆管内径,空气阻力及各处摩擦均不计,求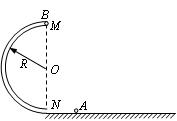
(1)粘合后的两球从飞出轨道到落地的时间t;
(2)小球A冲进轨道时速度v的大小。
(3)小球A与小球B球碰撞前瞬间对轨道的压力多大?方向如何?
如图所示,一质量为M=1.2kg的物块静止在桌面边缘,桌面离水平地面的高度为h=1.8m。一质量为m=20g的子弹以水平速度v0=100m/s射入物块,在很短的时间内以水平速度穿出。已知物块落地点离桌面边缘的水平距离x为0.9m,取重力加速度g=10m/s2,求子弹穿出物块时速度v的大小。
如图所示,一个半径为R的 透明圆柱体放置在水平面上,一束蓝光从A点沿水平方向射入圆柱体后经B点射出,最后射到水平面上的C点。已知OA=
透明圆柱体放置在水平面上,一束蓝光从A点沿水平方向射入圆柱体后经B点射出,最后射到水平面上的C点。已知OA= ,该圆柱体对蓝光的折射率为
,该圆柱体对蓝光的折射率为 ,则:
,则: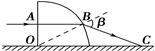
①它从圆柱面射出时的出射角β为多大?
②若换用一束红光同样从A点射向该圆柱体,则它从圆柱体射出后在水平面上形成的光点在C点的哪侧?
如图所示,一直立的汽缸用一质量为m的活塞封闭一定质量的理想气体,活塞横截面积为S,气体最初的体积为V0,气体最初的压强为p0/2,汽缸内壁光滑且缸壁是导热的。开始活塞被固定,打开固定螺栓K,活塞下落,经过足够长时间后,活塞停在B点,设周围环境温度保持不变,已知大气压强为p0,重力加速度为g。若一定质量理想气体的内能仅由温度决定,求:
①活塞停在B点时缸内封闭气体的体积V;
②整个过程中通过缸壁传递的热量Q。