下图是《驾驶员守则》中的安全距离图示和部分安全距离表格: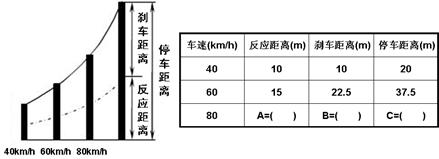
请根据图表计算
⑴如果驾驶员的反应时间一定,请在表格中填上A的数据;
⑵如果路面情况相同,请在表格中填上B、C的数据;
⑶如果路面情况相同,一名喝了酒的驾驶员发现前面50m处有一队学生正在横穿马路,此时他的车速为72km/h,而他的反应时间比正常时慢了0.1s,请问他能在50m内停下来吗?
如图所示,MNPQ是一块正方体玻璃砖的横截面,其边长MN =" MQ" = 30 cm。与MNPQ在同一平面内的一束单色光AB射到玻璃砖MQ边的中点B后进入玻璃砖,接着在QP边上的F点(图中未画出)发生全反射,再到达NP边上的D点,最后沿DC方向射出玻璃砖。已知图中∠ABM = 30°,PD =" 7.5" cm,∠CDN = 30°。
①画出这束单色光在玻璃砖内的光路图,求出QP边上的反射点F到Q点的距离QF;
②求出该玻璃砖对这种单色光的折射率;(结果可用根式表示,下同)
③求出这束单色光在玻璃砖内的传播速度(已知真空中光速c = 3×108 m/s)。
如图所示,两个绝热、光滑、不漏气的活塞A和B将气缸内的理想气体分隔成甲、乙两部分,气缸的横截面积为S =" 500" cm2。开始时,甲、乙两部分气体的压强均为1 atm(标准大气压)、温度均为27 ℃,甲的体积为V1 =" 20" L,乙的体积为V2 =" 10" L。现保持甲气体温度不变而使乙气体升温到127 ℃,若要使活塞B仍停在原位置,则活塞A应向右推多大距离?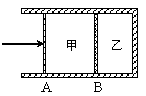
如图所示,位于竖直平面内的坐标系xOy,在其第三象限空间有正交的匀强磁场和匀强电场,匀强磁场沿水平方向且垂直于纸面向外、磁感应强度大小为B,匀强电场沿x 轴负方向、场强大小为E。在其第一象限空间有沿y 轴负方向的、场强大小为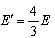 的匀强电场。一 个电荷量的绝对值为q 的油滴从图中第三象限的P 点得到一初速度,恰好能沿PO 作直线运动(PO 与x 轴负方向的夹角为θ = 37°),并从原点O 进入第一象限。已知重力加速度为g,sin37°= 0.6,cos37°= 0.8,不计空气阻力。问:
的匀强电场。一 个电荷量的绝对值为q 的油滴从图中第三象限的P 点得到一初速度,恰好能沿PO 作直线运动(PO 与x 轴负方向的夹角为θ = 37°),并从原点O 进入第一象限。已知重力加速度为g,sin37°= 0.6,cos37°= 0.8,不计空气阻力。问: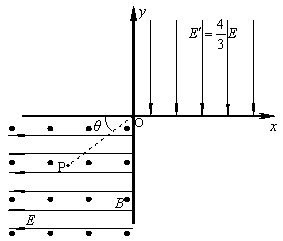
(1)油滴的电性;
(2)油滴在P 点得到的初速度大小;
(3)在第一象限的某个长方形区域再加上一个垂直于纸面向里的、磁感应强度也为B 的匀强磁场,且该长方形区域的下边界在x 轴上,上述油滴进入第一象限后恰好垂直穿过x 轴离开第一象限,求这个长方形区域的最小面积以及油滴在第一象限内运动的时间。
如图所示,在倾角为θ = 37°的固定长斜面上放置一质量M =" 1" kg、长度L1 =" 3" m 的极薄平板 AB,平板的上表面光滑,其下端 B 与斜面 底端C 的距离为L2 =" 16" m。在平板的上端A 处放一质量m =" 0.6" kg 的小滑块(视为质点),将小滑块和薄平板同时无初速释放。设薄平板与斜面之间、小滑块与斜面之间的动摩擦因数均为μ = 0.5,求滑块与薄平板下端B 到达斜面底端C 的时间差Δt。(已知sin37° = 0.6,cos37° = 0.8,取g =" 10" m/s2)
如图甲所示,在直角坐标系0≤x≤L区域内有沿y轴正方向的匀强电场,场强大小 ,右侧有一个以点(3L,0)为中心、边长为2L的正方形区域,其边界ab与x轴平行,正方形区域与x轴的交点分别为M、N。现有一质量为m,带电量为e的电子,从y轴上的A点以速度v0沿x轴正方向射入电场,飞出电场后从M点进入正方形区域。
,右侧有一个以点(3L,0)为中心、边长为2L的正方形区域,其边界ab与x轴平行,正方形区域与x轴的交点分别为M、N。现有一质量为m,带电量为e的电子,从y轴上的A点以速度v0沿x轴正方向射入电场,飞出电场后从M点进入正方形区域。

(1)求电子进入正方形磁场区域时的速度v;
(2)在正方形区域加垂直纸面向里的匀强磁场B,使电子从正方形区域边界点d点射出,则B的大小为多少;
(3)若当电子到达M点时,在正方形区域加如图乙所示周期性变化的磁场(以垂直于纸面向外为磁场正方向),最后电子运动一段时间后从N点飞出,速度方向与电子进入磁场时的速度方向相同,求正方形磁场区域磁感应强度B0的大小、磁场变化周期T各应满足的表达式。