本题满分10分)
一艘轮船按照北偏西50°的方向,以15海里每小时的速度航行,一个灯塔M原来在轮船的北偏东10°方向上,经过40分钟,轮船与灯塔的距离是 海里,则灯塔和轮船原来的距离为多少?
海里,则灯塔和轮船原来的距离为多少?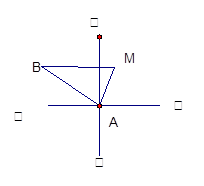
如图,已知圆心坐标为 的圆
的圆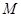 与
与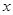 轴及直线
轴及直线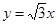 均相切,切点分别为
均相切,切点分别为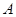 、
、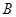 ,另一圆
,另一圆 与圆
与圆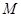 、
、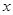 轴及直线
轴及直线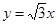 均相切,切点分别为
均相切,切点分别为 、
、 。
。
(1)求圆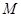 和圆
和圆 的方程;
的方程;
(2)过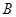 点作
点作 的平行线
的平行线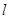 ,求直线
,求直线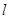 被圆
被圆 截得的弦的长度;
截得的弦的长度;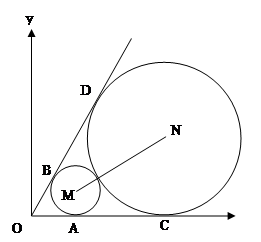
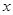
已知函数f(x)=mx2-mx-1.
(1)若对于x∈R,f(x)<0恒成立,求实数m的取值范围;
(2)若对于x∈[1,3],f(x)<5-m恒成立,求实数m的取值范围.
如图所示,在四棱锥 中,
中,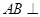 平面
平面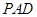 ,
,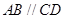 ,
, ,
,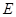 是
是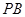 的中点,
的中点, 是
是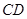 上的点且
上的点且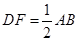 ,
,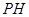 为△
为△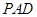 中
中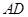 边上的高.
边上的高.
(1)证明: 平面
平面 ;
;
(2)若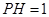 ,
, ,
,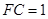 ,求三棱锥
,求三棱锥 的体积;
的体积;
(3)证明: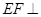 平面
平面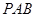 .
.
下图是淮北市6月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染.某人随机选择6月1日至6月15日中的某一天到达该市,并停留2天.
(1)求此人到达当日空气重度污染的概率;
(2)若设 是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
是此人停留期间空气质量优良的天数,请分别求当x=0时,x=1时和x=3时的概率值。
(3)由图判断从哪天开始淮北市连续三天的空气质量指数方差最大?(结论不要求证明)
如图,在△ABC中,∠ABC=90°,AB=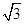 ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
(1)若PB=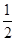 ,求PA;
,求PA;
(2)若∠APB=150°,求tan∠PBA.