已知函数f(x)在(-1,1)上有定义,f(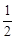 )=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(
)=-1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(-1,1)都有f(x)+f(y)=f(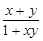 ),试证明:
),试证明:
(1)f(x)为奇函数;
(2)f(x)在(-1,1)上单调递减.
机器按照模具生产的产品有一些也会有缺陷,我们将有缺陷的产品称为次品,每小时出现的次品数随机器运转速度的不同而变化。下表为某机器生产过程的数据:
| 速度x(百转/秒) |
每小时生产次品数y(个) |
| 2 |
30 |
| 4 |
40 |
| 5 |
50 |
| 6 |
60 |
| 8 |
70 |
①求机器运转速度与每小时生产有缺点的产品数之间的回归方程
②若实际生产所允许的每小时生产有缺点的产品数不超过75件,那么机器的速度每秒不超过多少百转?(写出满足的整数解)
随着生活水平的提高,越来越多的人参与了潜水这项活动。某潜水中心调查了100名男姓与100名女姓下潜至距离水面5米时是否会耳鸣,下图为其等高条形图:
①绘出2×2列联表;②利用独立性检验方法判断性别与耳鸣是否有关系?若有关系,所得结论的把握有多大?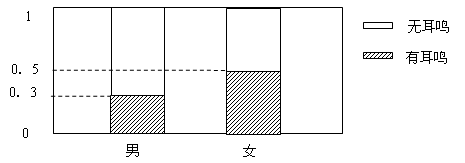
用反证法证明:如果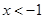 ,那么
,那么
已知复数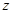 满足:
满足:  求
求 的值.
的值.
某初级中学共有学生2000名,各年级男、女生人数如下表:
| 初一年级 |
初二年级 |
初三年级 |
|
| 女生 |
373 |
x |
y |
| 男生 |
377 |
370 |
z |
已知在全校学生中随机抽取1名,抽到初二年级女生的概率是0.19.
(1)求x的值.
(2)现用分层抽样的方法在全校抽取48名学生,问应在初三年级抽取多少名?
(3)已知y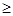 245,z
245,z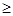 245,求初三年级中女生比男生多的概率.
245,求初三年级中女生比男生多的概率.