一列快车长70米,慢车长80米,若两车同向而行,快车从追上慢车到完全离开慢车所用时间为20秒;若两车相向而行,则两车从相遇到离开时间为4秒,求两车每秒钟各行多少米?
如图:
若设快车每秒钟行x米,慢车每秒行y米.
根据题意填空:
(1)若同向而行,经过20秒快车行驶路程比慢车行驶路程多____米,可列方程_________.
(2)若相向而行,两车4秒钟共行驶__________米,可列方程__________________.
(3)由以上可得方程组__________________,解得________.
先化简,再求值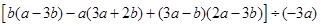 ,其中
,其中 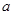 、
、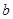 满足
满足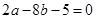 .
.
解方程(每题5分,共10分)
(1)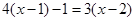
(2)
计算
(1)如图1,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E. 证明:DE=BD+CE.
如图2,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图3,D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状. 
若x²y+xy²=30,xy=6,求下列代数式的值:(1)x²+y²;(2)x-y.