出租车司机从饭店到火车站途中有六个交通岗，假设他在各交通岗到红灯这一事件是相互独立的，并且概率都是
（1）求这位司机遇到红灯前，已经通过了两个交通岗的概率；
（2）求这位司机在途中遇到红灯数ξ的期望和方差。
（本小题满分12分）已知函数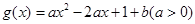
在区间[2，3]上有最大值4和最小值1，设
（1）求a、b的值；
（2）若不等式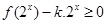
在
上有解，求实数k的取值范围
（本小题满分l2分）在△ABC中，角A，B，C所对的边分别为a，b，c，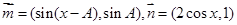
（x∈R）：’函数
在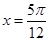
处取得最大值．
（1）当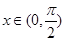
时，求函数
的值域；
（2）若a=7且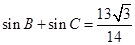
，求△ABC的面积
（本小题满分12分） 设a1，d为实数，首项为a1，公差为d的等差数列{an}的前n项和为Sn，满足S5S6+15=0，S5="5" ；
（1）求通项an及Sn；
（2）设
是首项为1，公比为3的等比数列．求数列{bn}的通项公式及其前n项和Tn。
（本小题满分14分）已知数列{an}满足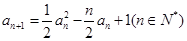
且a1=3。
（1）求a2，a3，a4的值及数列{an}的通项an；
（2）设数列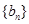
满足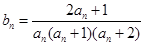
，Sn为数列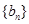的前n项和，求证：
。
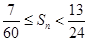（本小题满分13分）已知函数
为自然对数的底数）
（1）求函数
的最小值；
（2）若≥0对任意的x∈R恒成立，求实数a的值；
（3）在（2）的条件下，证明：