(本小题满分12分)已知函数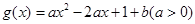 在区间[2,3]上有最大值4和最小值1,设
在区间[2,3]上有最大值4和最小值1,设
(1)求a、b的值;
(2)若不等式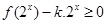 在
在 上有解,求实数k的取值范围
上有解,求实数k的取值范围
已知△ABC中,A,B,C所对的边分别为a,b,c,已知m=(sin C,sin Bcos A),n=(b,2c),且m·n=0.
(1)求A的大小;
(2)若a=2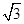 ,c=2,求△ABC的面积S的大小.
,c=2,求△ABC的面积S的大小.
设等差数列{an}满足a3=5,a10=-9.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn及使得Sn最大的序号n的值.
设锐角三角形ABC的内角A、B、C的对边分别为a、b、c,a=2bsin A.
(1)求角B的大小;
(2)若a=3 ,c=5,求b.
,c=5,求b.
本题共有3个小题,第1小题4分,第2小题5分,第3小题5分.
设等比数列 的前
的前 项的和为
项的和为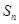 ,公比为
,公比为 .
.
(1)若 成等差数列,求证:
成等差数列,求证: 成等差数列;
成等差数列;
(2)若 (
(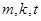 为互不相等的正整数)成等差数列,试问数列
为互不相等的正整数)成等差数列,试问数列 中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
中是否存在不同的三项成等差数列?若存在,写出两组这三项;若不存在,请说明理由;
(3)若 为大于
为大于 的正整数.试问
的正整数.试问 中是否存在一项
中是否存在一项 ,使得
,使得 恰好可以表示为该数列中连续两项的和?请说明理由.
恰好可以表示为该数列中连续两项的和?请说明理由.
本题共有2个小题,第1小题6分,第2小题6分
在上海自贸区的利好刺激下, 公司开拓国际市场,基本形成了市场规模;自2014年1月以来的第
公司开拓国际市场,基本形成了市场规模;自2014年1月以来的第 个月(2014年1月为第一个月)产品的内销量、出口量和销售总量(销售总量=内销量
个月(2014年1月为第一个月)产品的内销量、出口量和销售总量(销售总量=内销量 出口量)分别为
出口量)分别为 、
、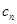 和
和 (单位:万件),依据销售统计数据发现形成如下营销趋势:
(单位:万件),依据销售统计数据发现形成如下营销趋势: ,
,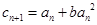 (其中
(其中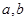 为常数,
为常数, ),已知
),已知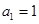 万件,
万件, 万件,
万件, 万件.
万件.
(1)求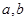 的值,并写出
的值,并写出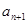 与
与 满足的关系式;
满足的关系式;
(2)证明: 逐月递增且控制在2万件内.
逐月递增且控制在2万件内.