(本小题满分13分)已知椭圆C: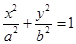 (a>b>0)的两个焦点分别为F1(-
(a>b>0)的两个焦点分别为F1(- ,0)、F2(
,0)、F2( ,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
,0).点M(1,0)与椭圆短轴的两个端点的连线相互垂直.
(1)求椭圆C的方程;
(2)已知点N的坐标为(3,2),点P的坐标为(m,n)(m≠3).过点M任作直线l与椭圆C相交于A、B两点,设直线AN、NP、BN的斜率分别为k1、k2、k3,若k1+k3=2k2,试求m,n满足的关系式.
已知函数 ,
, ,
,
(Ⅰ)当 时,若
时,若 在
在 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;
(Ⅱ)求满足下列条件的所有实数对 :当
:当 是整数时,存在
是整数时,存在 ,使得
,使得 是
是 的最大值,
的最大值, 是
是 的最小值;
的最小值;
(Ⅲ)对满足(Ⅱ)的条件的一个实数对 ,试构造一个定义在
,试构造一个定义在 ,且
,且 上的函数
上的函数 ,使当
,使当 时,
时, ,当
,当 时,
时, 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以 为首项的等差数列。
为首项的等差数列。
已知:函数
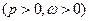 的最大值为
的最大值为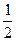 ,最小正周期为
,最小正周期为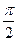 .
.
(Ⅰ)求: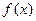 的解析式;
的解析式;
(Ⅱ)若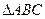 的三条边为
的三条边为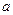 ,
,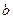 ,
,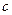 ,满足
,满足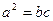 ,
,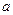 边所对的角为
边所对的角为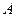 .求:角
.求:角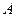 的取值范围及函数
的取值范围及函数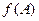 的值域.
的值域.
已知集合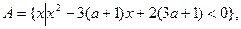
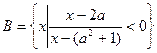 ,
,
(Ⅰ)当 时,求
时,求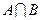 ;
;
(Ⅱ)求使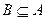 的实数
的实数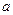 的取值范围。
的取值范围。
已知函数 的图象过坐标原点O,且在点
的图象过坐标原点O,且在点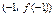 处的切线的斜率是
处的切线的斜率是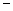 5.
5.
(1)求实数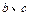 的值;
的值;
(2)求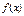 在区间
在区间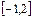 上的最大值;
上的最大值;
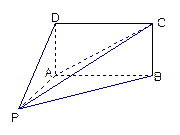
如图,四棱锥P-ABCD的底面ABCD为矩形,且PA="AD=1,AB=2," 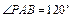 ,
,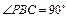 .
.
(1)求证:平面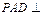 平面
平面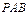 ;
;
(2)求三棱锥D-PAC的体积;
(3)求直线PC与平面ABCD所成角的正弦值.