(本小题满分13分)已知函数 为自然对数的底数)
为自然对数的底数)
(1)求函数 的最小值;
的最小值;
(2)若 ≥0对任意的x∈R恒成立,求实数a的值;
≥0对任意的x∈R恒成立,求实数a的值;
(3)在(2)的条件下,证明:
已知函数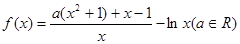 .
.
(1) 当 时,讨论
时,讨论 的单调性;
的单调性;
(2)设 ,当
,当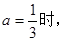 若对任意
若对任意 存在
存在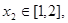 使
使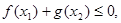 求实数
求实数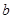 的取值范围。
的取值范围。
如图,椭圆
 的焦点在x轴上,左右顶点分别为
的焦点在x轴上,左右顶点分别为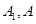 ,上顶点为B,抛物线
,上顶点为B,抛物线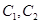 分别以A,B为焦点,其顶点均为坐标原点O,
分别以A,B为焦点,其顶点均为坐标原点O, 与
与 相交于直线
相交于直线 上一点P.
上一点P.
(1)求椭圆C及抛物线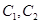 的方程;
的方程;
(2)若动直线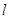 与直线OP垂直,且与椭圆C交于不同的两点M,N,已知点
与直线OP垂直,且与椭圆C交于不同的两点M,N,已知点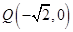 ,求
,求 的最小值。
的最小值。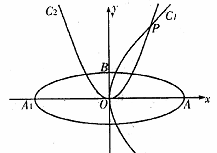
已知圆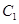 的方程为
的方程为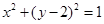 ,定直线
,定直线 的方程为
的方程为 .动圆
.动圆 与圆
与圆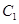 外切,且与直线
外切,且与直线 相切.
相切.
(1)求动圆圆心 的轨迹
的轨迹 的方程;
的方程;
(2)直线 与轨迹
与轨迹 相切于第一象限的点
相切于第一象限的点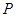 , 过点
, 过点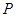 作直线
作直线 的垂线恰好经过点
的垂线恰好经过点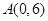 ,并交轨迹
,并交轨迹 于异于点
于异于点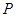 的点
的点 ,求直线
,求直线 的方程及
的方程及 的长.
的长.
已知四棱锥 ,底面
,底面 为矩形,侧棱
为矩形,侧棱 ,其中
,其中 ,
,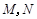 为侧棱
为侧棱 上的两个三等分点,如下图所示.
上的两个三等分点,如下图所示.
(1)求证: ;
;
(2)求异面直线 与
与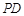 所成角的余弦值;
所成角的余弦值;
(3)求二面角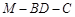 的余弦值.
的余弦值.
函数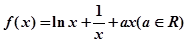
(1)a=0时,求f(x)最小值;
(2)若f(x)在 是单调减函数,求a的取值范围.
是单调减函数,求a的取值范围.