要制造一种机器零件，甲机床废品率为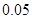
，而乙机床废品率为
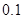，而它们
的生产是独立的，从它们制造的产品中，分别任意抽取一件，求：
（1）其中至少有一件废品的概率；（2）其中至多有一件废品的概率.
（本小题满分12分）一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如右表（单（辆）位: 按类型分层抽样的方法在这个月生产的轿车中抽取50辆, 其中有A类轿车10辆.
（1）求z的值.
（2）用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
（本小题满分12分）已知
ABC中,角A,B,C的对边分别为a,b,c, 若向量
与向量
共线.
（1）求角C的大小;
（2）若
,求
的值
（本小题14分）已知函数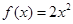
，
。
（1）设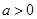
，若不等式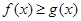
恒成立，求实数
的取值范围；
（2）令
，若
在
内的值域为闭区间，求实数的取值范围；
（3）求证：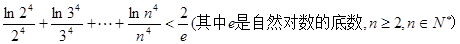
（本小题13分）已知函数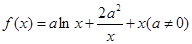
。
（1）若函数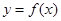
在点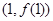
处的切线与直线
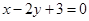垂直，求实数
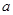的值；
（2）讨论函数
的单调性；
（3）当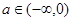
时，记函数的最小值为
，求证：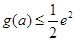
。
（本小题12分）设函数
，
（1）求
的周期和对称中心；
（2）求在
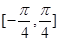上值域.