如图,棱柱 的侧面
的侧面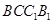 是菱形,
是菱形,

(Ⅰ)证明:平面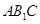
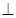 平面
平面 ;
;
(Ⅱ)设 是
是 上的点,且
上的点,且 平面
平面 ,求
,求 的值.
的值.
已知数列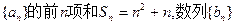 满足
满足 且
且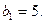
(I)求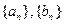 的通项公式;
的通项公式;
(II)设数列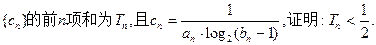
函数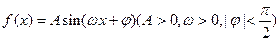 的部分图象如图所示。
的部分图象如图所示。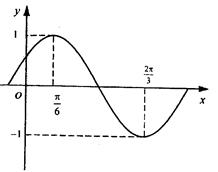
(I)求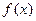 的最小正周期及解析式;
的最小正周期及解析式;
(II)设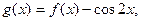 求函数
求函数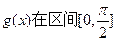 上的最大值和最小值
上的最大值和最小值
(本小题满分15分)
已知函数
(I)当 的单调区间;
的单调区间;
(II)若函数 的最小值;
的最小值;
(III)若对任意给定的 ,使得
,使得 的取值范围。
的取值范围。
过点M(4,2)作x轴的平行线被抛物线 截得的弦长为
截得的弦长为 。
。
(I)求p的值;
(II)过抛物线C上两点A,B分别作抛物线C的切线
(i)若 交于点M,求直线AB的方程;
交于点M,求直线AB的方程;
(ii)若直线AB经过点M,记 的交点为N,当
的交点为N,当 时,求点N的坐标
时,求点N的坐标
(本小题满分14分)
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,D,E分别为AB,CD的中点,AE的延长线交CB于F。现将△ACD沿CD折起, 折成二面角A—CD—B,连接AF。
(I)求证:平面AEF⊥平面CBD;
(II)当AC⊥BD时,求二面角A—CD—B大小的余弦值