(本小题满分15分)
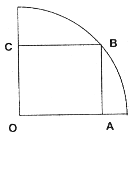
如图,在半径为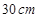 的
的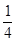 圆形(
圆形(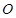 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料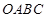 ,其中点
,其中点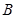 在圆上,点
在圆上,点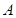 、
、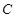 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮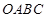 卷成一个以
卷成一个以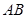 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长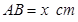 ,圆柱的体积为
,圆柱的体积为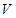
 .
.
(1)写出体积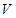 关于
关于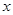 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当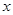 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积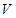 最大?最大体积是多少?
最大?最大体积是多少?
若定义在R上的函数 对任意的
对任意的 ,都有
,都有 成立,且当
成立,且当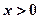 时,
时,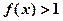 。
。
(1)求证: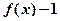 为奇函数;
为奇函数;
(2)求证: 是R上的增函数;
是R上的增函数;
(3)设集合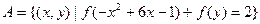 ,
, ,且
,且 , 求实数
, 求实数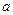 的取值范围。
的取值范围。
(本题12分)若二次函数满足 。
。
(1) 求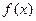 的解析式;
的解析式;
(2) 若在区间[-1,1]上不等式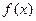 >2x+m恒成立,求实数m的取值范围。
>2x+m恒成立,求实数m的取值范围。
已知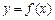 是定义在R上的函数,对于任意的
是定义在R上的函数,对于任意的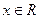 ,
, ,且当
,且当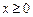 时,
时,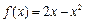 .
.
(1)求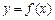 的解析式;
的解析式;
(2)画出函数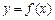 的图象,并指出
的图象,并指出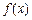 的单调区间及在每个区间上的增减性;
的单调区间及在每个区间上的增减性;
(3)若函数f(x)在区间[-1,a-2]上单调递增,试确定a的取值范围.
函数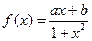 是定义在
是定义在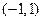 上的奇函数,且
上的奇函数,且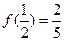 ,
,
(1)确定函数 的解析式;
的解析式;
(2)判断 在
在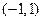 上的单调性并用定义证明.
上的单调性并用定义证明.
(3)解不等式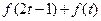 <0;
<0;
已知函数 .
.
(1)求实数 的范围,使
的范围,使 在区间
在区间 上是单调函数。 (2)求
上是单调函数。 (2)求 的最小值。
的最小值。