设函数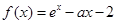 ,
,
(1)求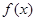 的单调区间
的单调区间
(2)若 为整数,且当
为整数,且当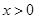 时,
时,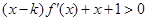 ,求
,求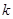 的最大值.
的最大值.
已知函数 ,
,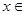 R.
R.
(1)求它的振幅、周期、初相;
(2)该函数的图象可由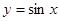 (
(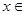 R)的图象经过怎样的平移和伸缩变换得到?
R)的图象经过怎样的平移和伸缩变换得到?
已知函数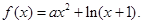
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)任意 ,
, 恒成立,求实数
恒成立,求实数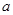 的取值范围.
的取值范围.
已知函数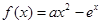
 .
.
(1)当 时,证明:
时,证明: 在
在 上为减函数;
上为减函数;
(2)若 有两个极值点
有两个极值点 求实数
求实数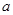 的取值范围.
的取值范围.
在某校组织的一次篮球定点投篮测试中,规定每人最多投 次,每次投篮的结果相互独立.在
次,每次投篮的结果相互独立.在 处每投进一球得
处每投进一球得 分,在
分,在 处每投进一球得
处每投进一球得 分,否则得
分,否则得 分. 将学生得分逐次累加并用
分. 将学生得分逐次累加并用 表示,如果
表示,如果 的值不低于
的值不低于 分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在
分就认为通过测试,立即停止投篮,否则继续投篮,直到投完三次为止.投篮的方案有以下两种:方案1:先在 处投一球,以后都在
处投一球,以后都在 处投;方案2:都在
处投;方案2:都在 处投篮.甲同学在
处投篮.甲同学在 处投篮的命中率为
处投篮的命中率为 ,在
,在 处投篮的命中率为
处投篮的命中率为 .
.
(Ⅰ)甲同学选择方案1.
求甲同学测试结束后所得总分等于4的概率;
求甲同学测试结束后所得总分 的分布列和数学期望
的分布列和数学期望 ;
;
(Ⅱ)你认为甲同学选择哪种方案通过测试的可能性更大?说明理由.
已知函数 ,
,
(1) 当 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;
(2)求函数 的单调区间.
的单调区间.