(本小题满分12分)如图1,渔船甲位于岛屿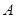 的南偏西
的南偏西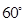 方向的
方向的 处,且与岛屿
处,且与岛屿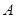 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿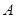 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从 处出发沿北偏东
处出发沿北偏东 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.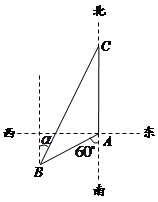
(1)求渔船甲的速度;
(2)求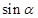 的值.
的值.
已知 为等比数列,
为等比数列,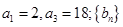 是等差数列,
是等差数列,
(Ⅰ)求数列 的通项公式及前
的通项公式及前 项和
项和 ;
;
(2)设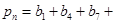
 ,
,
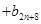 ,其中
,其中 ,试比较
,试比较 与
与 的大小,并加以证明.
的大小,并加以证明.
如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点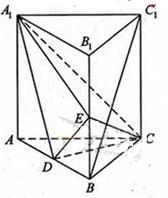
(Ⅰ)证明:BC1//平面A1CD;
(Ⅱ)设AA1=AC=CB=2,AB=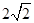 ,求三棱锥C一A1DE的体积.
,求三棱锥C一A1DE的体积.
一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间 |
1 |
2 |
3 |
4 |
5 |
| 频率 |
0.1 |
0.4 |
0.3 |
0.1 |
0.1 |
从第一个学生开始买饭时计时.
(Ⅰ)求第2分钟末没有人买晚饭的概率;
(Ⅱ)估计第三个学生恰好等待4分钟开始买饭的概率.
已知角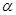 的顶点在原点,始边与
的顶点在原点,始边与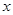 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点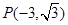 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若函数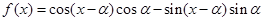 ,求函数
,求函数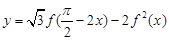 在区间
在区间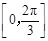 上的取值范围.
上的取值范围.
已知函数 (
(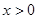 ,
,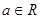 ),
),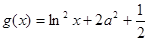 .
.
(Ⅰ)证明:当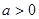 时,对于任意不相等的两个正实数
时,对于任意不相等的两个正实数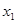 、
、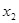 ,均有
,均有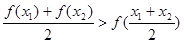 成立;
成立;
(Ⅱ)记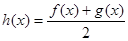 ,
,
(ⅰ)若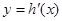 在
在 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
(ⅱ)证明: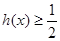 .
.