一中食堂有一个面食窗口,假设学生买饭所需的时间互相独立,且都是整数分钟,对以往学生买饭所需的时间统计结果如下:
| 买饭时间 |
1 |
2 |
3 |
4 |
5 |
| 频率 |
0.1 |
0.4 |
0.3 |
0.1 |
0.1 |
从第一个学生开始买饭时计时.
(Ⅰ)求第2分钟末没有人买晚饭的概率;
(Ⅱ)估计第三个学生恰好等待4分钟开始买饭的概率.
(本小题满分l2分)
如图,在多面体ABCDEF中,ABCD为菱形, ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA 面ABCD,G为BF的中点,若EG//面ABCD.
面ABCD,G为BF的中点,若EG//面ABCD.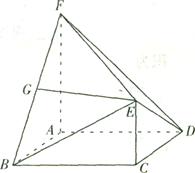
(1)求证:EG 面ABF;
面ABF;
(2)若AF=AB,求二面角B—EF—D的余弦值.
(本小题满分l0分)
已知圆 的圆心为
的圆心为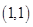 ,半径为
,半径为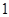 。直线
。直线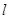 的参数方程为
的参数方程为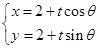 (
(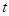 为参数),且
为参数),且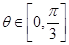 ,点
,点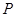 的直角坐标为
的直角坐标为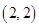 ,直线
,直线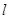 与圆
与圆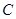 交于
交于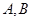 两点,求
两点,求 的最小值。
的最小值。
(本小题满分14分)
已知函数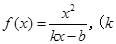 ,
,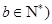 ,满足
,满足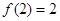 ,
,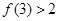 .
.
(1)求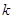 ,
,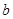 的值;
的值;
(2)若各项为正的数列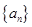 的前
的前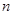 项和为
项和为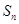 ,且有
,且有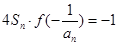 ,设
,设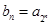 ,求数列
,求数列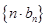 的前
的前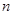 项和
项和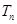 ;
;
(3)在(2)的条件下,证明: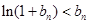 .
.
(本小题满分12分)
椭圆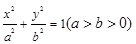 的左、右焦点分别为
的左、右焦点分别为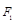 、
、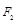 ,点
,点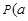 ,
,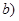 满足
满足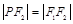 .
.
(1)求椭圆的离心率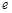 ;
;
(2)设直线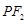 与椭圆相交于
与椭圆相交于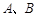 两点,若直线
两点,若直线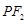 与圆
与圆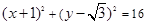 相交于
相交于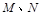 两点,且
两点,且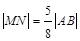 ,求椭圆的方程.
,求椭圆的方程.
(本小题满分13分)
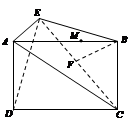
如图,四边形 为矩形,
为矩形,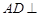 平面
平面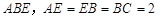 ,
,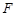 为
为 上的点,且
上的点,且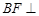 平面
平面 .
.
(1)求证: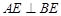 ;
;
(2)求三棱锥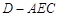 的体积;
的体积;
(3)设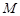 在线段
在线段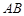 上,且满足
上,且满足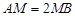 ,试在线段
,试在线段 上确定一点
上确定一点 ,使得
,使得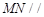 平面
平面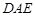 .
.