(本小题满分14分)
已知函数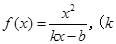 ,
,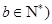 ,满足
,满足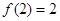 ,
,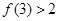 .
.
(1)求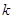 ,
,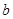 的值;
的值;
(2)若各项为正的数列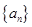 的前
的前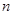 项和为
项和为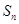 ,且有
,且有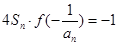 ,设
,设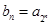 ,求数列
,求数列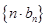 的前
的前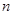 项和
项和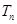 ;
;
(3)在(2)的条件下,证明: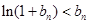 .
.
(本小题满分12分)为了了解《中华人民共国道路交通安全法》在学生中的普及情况,调查部门对某学校6名学生进行问卷调查,6人得分情况如下:5,6,7,8,9,10.把这6名学生的得分看成一个总体.
(1)求该总体的平均数;
(2)求该总体的的方差;
(3)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本,求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
(本小题满分12分)已知 ,
, .
.
(1)若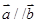 ,求
,求 的值;
的值;
(2)若 ,求
,求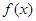 的单调递增区间.
的单调递增区间.
(本小题满分12分)已知向量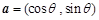 ,
, .
.
(1)若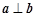 ,求
,求 的值;
的值;
(2)若 ,
, ,求
,求 的值
的值
(本小题满分12分)已知函数
(Ⅰ)求 最小正周期;
最小正周期;
(Ⅱ)求 在区间
在区间 上的最大值和最小值.
上的最大值和最小值.
(本小题满分12分)为了解甲、乙两校高三年级学生某次期末联考地理成绩情况,从这两学校中分别随机抽取30名高三年级的地理成绩(百分制)作为样本,样本数据的茎叶图如图所示: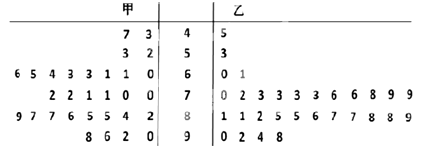
(Ⅰ)若乙校高三年级每位学生被抽取的概率为0.15,求乙校高三年级学生总人数;
(Ⅱ)根据茎叶图,分析甲、乙两校高三年级学生在这次联考中地理成绩;
(Ⅲ)从样本中甲、乙两校高三年级学生地理成绩不及格(低于60分为不及格)的学生中随机抽取2人,求至少抽到一名乙校学生的概率.