已知函数
(1)若对任意实数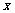 ,函数值恒大于零,求实数
,函数值恒大于零,求实数 的取值范围;
的取值范围;
(2)若函数有两个不同的零点,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知数列 的前n项和为
的前n项和为 ,点
,点 均在函数
均在函数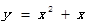 的图像上
的图像上
(1)求数列 的通项公式;
的通项公式;
(2)设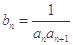 ,求数列
,求数列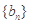 的前n项和
的前n项和
(本小题满分12分)已知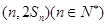 ,若
,若 是
是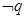 的充分而不必要条件,求实数
的充分而不必要条件,求实数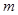 的取值范围.
的取值范围.
(本小题满分12分)已知等差数列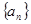 的第二项为8,前10项和为185.
的第二项为8,前10项和为185.
(1)求数列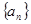 的通项公式;
的通项公式;
(2)若从数列 通项满足
通项满足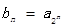 ,试求数列
,试求数列 的通项公式和前n项的和
的通项公式和前n项的和 .:
.:
(本小题满分12分)设有两个命题,命题P:不等式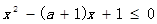 的解集是
的解集是 ;命题:函数
;命题:函数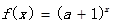 在定义域中是增函数,
在定义域中是增函数,
(1)若 为真命题时,求a的取值范围;
为真命题时,求a的取值范围;
(2)若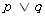 为真命题时,求a的取值范围.
为真命题时,求a的取值范围.